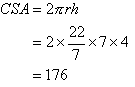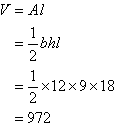Unit 5: Topic 3: Surface Area and Volume of Cylinders

Competencies

·   Determine the surface area of different types of cylinders

·   Calculate the volume of cylinders

Suggested ways of teaching this topic: teacher’s explanation using demo, Q & A, guided practice, independent practice

Starter Activities

The teacher shall start explaining the terms: radius, axis, base, curved surface and total surface using demo on a cylindrical object as shown below.

Expected Explanation

The radius of the circular cross-section is called the radius of the cylinder, and the straight line that passes through the center of each circular cross-section is called the axis of the cylinder. The length of the axis is called the height of the cylinder. Consider a cylinder of radius r and height h, the radius and height of the cylinder are represented by r and h respectively. The total surface area (TSA) includes the area of the circular top and base, as well as the curved surface area (CSA).

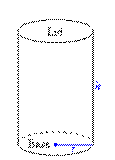
To determine a formula for the curved surface area of a cylindrical can, wrap a sheet of paper snugly around the can and tape it together. Trim the paper at the top and bottom to match the shape of the can. Then slide the paper off the can and cut this paper cylinder parallel to its axis so that it forms the rectangle shown in the above diagram.

Lesson Notes

As canbe seen from the above drawings, the length of the rectangle = circumference of the base circle

= 2πr

The width of the rectangle = height of the cylinder

= h

Therefore, the total surface area (TSA) of a cylinder with radius r and height h is given by

TSA = 2π(r + h)

Example: Find the total surface area of a cylindrical tin of radius 17 cm and height 3 cm.

Solution:

 

 

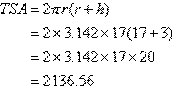
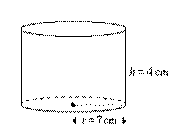
Example: Find the area of the curved surface of a cylindrical tin with radius 7 cm and height 4 cm.

Solution:

Volume of a Solid

The teacher may start with a question and answer session asking questions of the following type:

·         What do you think “volume” mean?

·         What is a prism? A cylinder?

Expected Replies

Volume is the amount of space occupied by a three-dimensional object; and it is measured in cubic units. The most frequently used units of volume are mm³, cm³ and m³.

A solid with parallel sides is called a prism. For example, solids such as a cube or a rectangular box are prisms.

The Volume V, of a solid is given by:

  Volume = Area of base x Height

V = Ah,

where A is the area of the base (cross-section) and h is the height

Since Grade 9 students are already familiar with the volumes of some solids in lower grades, the teacher shall use Q & A or independent practice to make students recall some of the formulae given below. The examples also could be given as independent practice recalling questions.

The volumes of the following solids are often required to solve real world problems involving quantity, capacity, mass and strength of materials including liquids.

Example: Find the volume of a cylindrical canister with radius 7 cm and height 12 cm.

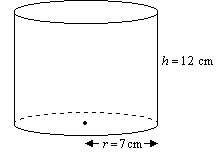Solution:

V = π r²h

= π7cm)²12 cm

= 588 π cm³

 

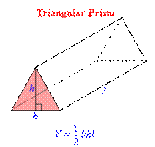
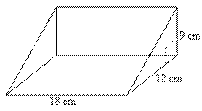
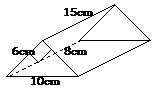
Example: Find the volume of the triangular prism shown in the diagram.

Solution:

 

 

Practice Exercises

1.       Calculate the volume and surface area of the solids shown in the figure below.

2.       Calculate the total surface area and volume of a cylinder whose

a)                  Height is 5 cm and base radius 4 cm

b)                  Height 5 cm and base diameter 6 cm

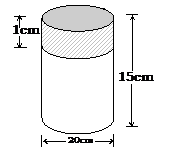
3.       The figure below shows a coffee can with a plastic lid. Calculate the surface area of the plastic lid. What could be the volume of the can below the lid?

4.       A cylindrical water tanker has the same length of height as its diameter. What are the volume and total surface area of such tanker?