Unit 5: Topic 2: Angle
Properties of Circles
Competencies
·
state angle properties of circles
·
apply angle properties of circles to solve related problems
Suggested ways
of teaching this topic: Guided practice,
Starter Activities
The
teacher could start with brainstorming questions like:
·
Define the terms: chord, diameter, radius, tangent, secant, arc
·
What is the relationship between diameter and any chord perpendicular to
that diameter?
Do you
agree with the following statements?
1)
In Equal circles or in the same circle equal chords are equidistant from
the center
2)
Chords which are equidistant from the center are equal
3)
Tangents from an external point are equal in length
Expected Answers
Chord: a line segment joining two points of a
circle or a line segment whose end points lie on the circle.
Diameter: the largest
chord through the center of a circle.
Radius: a line segment
drawn from the center to any point on the circle.
Tangent: any line which
touches the outer part of the circle at only one point.
Secant: any line that
cuts a circle in to two.
The diameter bisects any chord perpendicular to it.
Yes! All the statements are correct.
Angle
Properties of Circles
The
teacher shall revise also on the meanings of major and minor arcs, angle
subtended by an arc and arcs intercepted by an angle using short Q & A with
students. Then, it would be appropriate time to discuss the following four angle
properties of circles using guided practice:
(1) Angle at Centre
(2) Angle in Semicircle
(3) Angles in Same Segment
(4) Angles in Opposite Segments
Lesson
Notes
An inscribed
angle is an angle whose vertex is on the circumference of a circle, and
whose sides contain chords of the circle.
An angle
intercepts an arc if:
·
The
END-POINTS of the arc lie on the angle
·
Each
SIDE of the angle contains at least one end -point of the arc
·
Except
for its end -points, the arc lies in the interior of the angle.
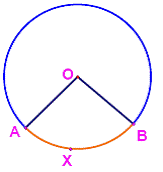
Theorem:
The
measure of an angle inscribed in a circle is half of the measure of the arc subtending
it.
m(![]() ABC)= ½ m(arc AXC)
ABC)= ½ m(arc AXC)
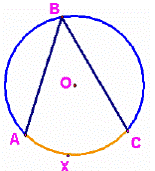
Theorem:
An
angle inscribed in a semi -circle is a right angle. The converse of this
corollary is that a circular arc in which a right angle is inscribed must be a
semi -circle.
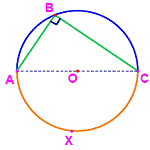
m(![]() ABC)= ½ m(arc AXC) = 900
ABC)= ½ m(arc AXC) = 900
Theorem: Angles inscribed
in the same arc must be congruent.
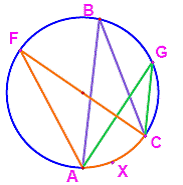
m(
![]() ABC)= m(
ABC)= m( ![]() AFB) =m(
AFB) =m( ![]() AGC)= = ½ m(arc AXC)
AGC)= = ½ m(arc AXC)
Theorem:
An
angle inscribed in an arc LESS than a semi -circle will be OBTUSE, i.e. greater
than 900. An angle inscribed in an arc GREATER than a semi -circle
will be ACUTE.
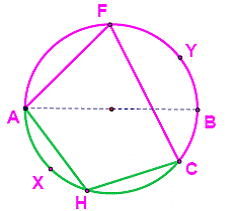
Theorem:
The
angle formed by a tangent and a chord drawn from the point of tangency is
measured by half the arc it intercepts.
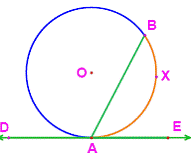
Theorem: The measure of
the angle formed by two intersecting chords is half the sum of the measures of
the arc intercepted by the angle and its vertically opposite angle.
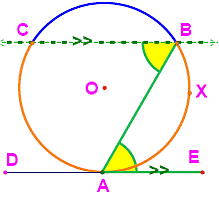
Theorem: The point of
intersection separates the chord into 2 segments. The product of the lengths of
the segments for one chord is the same as the product for the other chord.
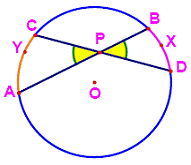
Theorem:
The
measure of an angle formed by 2 secants is one -half of the difference of the
measure of the intercepted arcs.
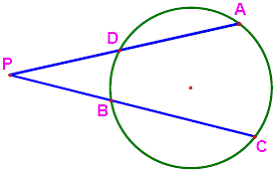
Practice Exercise
1. Given Circle O, as shown,

a)
Name one minor arc in the circle.
b)
Name one major arc in the circle.
c)
Name the angle subtended at the centre by arc BD.
d)
Name the inscribed angle subtended by arc BD.
e)
An angle in a semi-circle.
f)
2 angles subtended by chord AB.
2. Given: Circle with centre O, as
shown below, with m(∠DOB) = 86 °
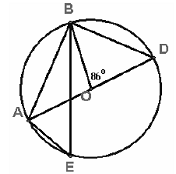
Calculate:
a)
m(∠DAB)
b)
m(∠AOB)
c)
m(∠ABD)
d)
m(∠ODB)
e)
m(∠ AEB)
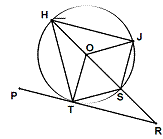
3. Given circle with center O, as shown in the
figure, if m(arc HT)=m(arc HJ) and m(∠PTH)=
58, calculate the measure of the remaining
angles or arcs.
4. In the figure below m(arc AC)=m(arc CF),
m(∠AGF)= 420 and m(∠GCF)= 250.
Calculate
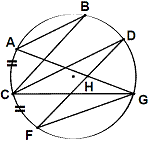
a) m(∠ABC)
b) m(∠DHG)