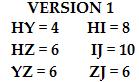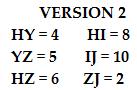Unit 5: Geometry and Measurement

Topic 1: Triangle Similarity Theorems

Competencies

· State similarity triangle theorems

· Apply similarity triangle theorems

· Apply similarity ratio on similar triangles

Suggested ways of teaching this topic: Guided practice, Q&A, small group discussion,…

Starter Activities

The teacher may start with the brainstorming question like:

· Who can tell me the definition of similar triangles? Or

· When do we say two triangles are similar?

· What kind of symbol do we use to denote similarity?

· Who can demonstrate the similarity of two triangles in drawing?

Expected Answer

Triangles are similar if their corresponding (matching) angles are congruent (equal) and the corresponding sides are in same proportion.

The Symbol for Similar is:

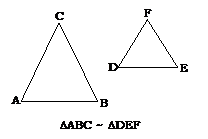
When we say DABC ~ DDEF,

The 3 corresponding angles are congruent

i.e. ÐA ºÐD, ÐB ºÐE, ÐC ºÐF

The 3 corresponding sides are in proportion

i.e.

The teacher shall ask the following question to make sure students understood the idea of proportional sides in similar triangles.

· If DABC ~ DXYZ then list down as many proportional equations as you can.

Expected Answer:

DABC ~ DXYZ Þ

What is similarity ratio?

The similarity ratio is the proportion that you get when you divide any corresponding side of one triangle by its corresponding side in other similar triangle.

Lesson Notes

The teacher shall use the following examples to let students have a better practice on finding ratio of sides in similar triangles.

Example: Let DABC ~ DEFD as shown in the figure. Find the length of

Solution: DABC ~ DEFD Þ

ÞÞ ED = = 16cm

DABC ~ DEFD ÞÞ

ÞÞ FD = = 20cm

Example: In the figure, if DABC ~ DADE, What is the length of AC?

Solution: DABC ~ DADE Þ

EC = 6.4 – 4 = 2.4cm

AC = AE + EC

= 4 + 2.4 = 6.4cm

The teacher should ask students about the relationship between congruent and similar triangles. The following example might help.

Example: Prove that if DABC ºDDEF, then DABC ~ DDEF

Proof: DABC ºDDEF Þ AB = DE, BC = EF and AC = DF

Þ=1

That is, if two triangles are congruent then they are similar.

Teacher can ask students: “Is the converse statement true?”

Expected Answer

In similar triangles, only the angles are congruent but the sides are not necessarily congruent. Therefore, similar triangles may not be congruent.

Property of a line parallel to a side of a triangle

If a line parallel to a side of a triangle is drawn between the side and the opposite angle, then it divides the other two sides proportionally

That is, or

After a thorough discussion on the similarity ratio, the teacher may guide students with the following similarity theorems, their proofs and applications.

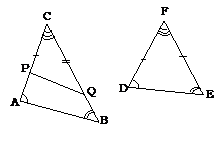
The AAA Theorem

If all the three angles of DABC is congruent to the corresponding angles of DDEF,

DABC ~ DDEF

Proof

Given: DABC and DDEF withÐA ºÐD, ÐB ºÐE and ÐC ºÐF

To prove: DABC ~ DDEF

Assume that AC > DF and BC > EF and mark points P and Q on such that PC = DF and QC = EF

Statement Reason

1. 1. Construction

2. ÐC ºÐF 2. Given

3. 3. Construction

4. DPCQ ºDDFE 4. SAS postulate

5. ÐCPQºÐD and ÐCQPºE 5. Corresponding angles of congruent triangles

6. ÐCPQºÐA and ÐCQPºÐB 6. Transitivity of congruence of angles

7. 7. Corresponding sides of congruent triangles

8. 8. Property of a line parallel to side of a triangle

9. 9. Substitution

Similarly,

Since the corresponding angles are congruent and the corresponding sides are proportional, we have DABC ~ DDEF.

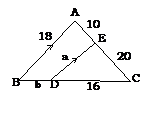
Example: In the figure, if Calculate a, b and c

Solution: ∆ECD ≡ ∆ACB by AAA

Theorem: (AA theorem)

If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.

The teacher could leave the proof to the students giving the clue that they can use the previous AAA Theorem.(Of course, they shall use angle sum theorem of triangles!)

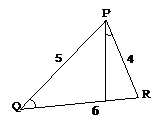Example: In the figure, if PQ = 5, QR = 6, PR = 4 and ÐPQR ºÐRPK, find KR and KP.

Solution:

Statement Reason

1. ÐR ºÐR 1. Common angle

2. ÐPQR ºÐRPK 2. Given

3. DRQP ~ DRPK 3. AA similarity theorem

The SAS Similarity Theorem

If two sides of a triangle are proportional to two sides of another triangle and the angle included in these sides are congruent, then the triangles are similar.

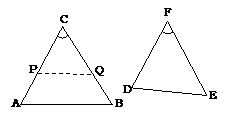Proof:

Given:DABC and DDEF with

ÐC º F,

To prove:DABC ~ DDEF

Construction: Assume AC > DF and BC > EF. Mark points P and Q on and respectively such that and

Statement Reason

1. 1. Construction

2. ÐC ºÐF 2. Given

3. 3. Construction

4. DPQC ºDDEF 4. SAS postulate

5. 5. Given

6. 6. Substitution

7. 7. property of propotional line segments

8. ÐCPQ ºÐA, ÐCQP ºÐB 8. Corresponding angles

9. ÐD ºÐA, ÐE ºÐB 9. Substitution

10. DABC ~ DDEF 10. AA similarity theorem

Example: Are the given pairs of triangles similar?

Solution:

A) congruent angles: ÐR ºÐL

Sides in proportion:

Therefore, DPQR ~ DNML since ÐR ºÐL and

B) m(ÐL) = 180⁰ – (65⁰ + 60⁰) = 55⁰ = m(ÐR)

Therefore, DPQR is not similar to DKLM

The SSS Similarity Theorem

If three sides of one triangle are proportion to three sides of another triangle, then the two triangles are similar.

Proof

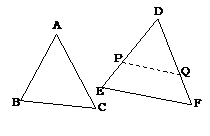Given: DABC and DDEF, With

To prove: DABC ~ DDEF

Construction: Assume that DE > AB and DF > AC.

Make point P on_{such that}. Then draw a line parallel tomeet DF at Q.

Statement Reason

1. ÐDPQ ºÐDEF 1. Corresponding angles

2. ÐD ºÐD 2. Common angle

3. DDPQ ~ DDEF 3. AA similarity theorem.

4. 4. Def. of similar triangles.

5. 5. Given

6. 6. Steps 4 & 5 and substitution

7. DABC ºDDPQ 7. SSS theorem

8. DABC ~ DDEF 8. Step 3 and substitution

Concluding Activities

The teacher shall make sure that the following are summarized by the students. The applications of the theorems are also well practiced through teacher supervised exercises.

§ Two triangles are said to be similar if all their corresponding angles are congruent and the corresponding sides are proportional.

§ The AA similarity theorem: If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.

§ The SAS Similarity Theorem: If two sides of a triangle are proportional to two sides of another triangle and the angle included in these sides is congruent, then the triangles are similar.

§ The SSS Similarity Theorem: If three sides of one triangle are proportional to three sides of another triangle, then the two triangles are similar.

§ Congruent triangles are similar but similar triangles may not be congruent.

Practice Exercises

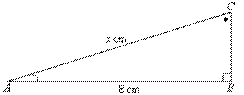
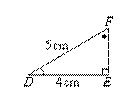
1. Find the value of x in the following pair of triangles.

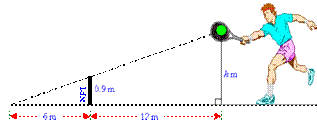
2. Find the value of the height, h m, in the following diagram at which the tennis ball must be hit so that it will just pass over the net and land 6 m away from the base of the net.

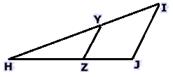
3. Below are two versions of ΔHIZ and ΔHYZ. Which of these two versions give a pair of similar triangles?

4. In the figure, ΔTUV and ΔTWX are similar withTU = 10 and TW = 40, what is the similarity ratio?

5. In the following figure, ED // BC. A, B and E are collinear and A, C and D are also collinear. Find AC and AB