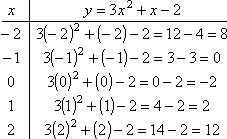Back Home Top Next

Unit 4: Topic 4: Graphs of Quadratic Functions

Competencies

·         sketch graphs of quadratic functions

·         determine vertical axis and turning point of the graph of quadratic functions without sketching

Suggested ways of teaching this topic: Guided practice

Starter Activities

The teacher may begin with questions of the following type:

·         What is the general form of quadratic equation?

·         Who will show me completing the square for f(x) = x2 + 6x – 4?

·         Who can sketch the graph of f(x) = 2x?

·         How do you find x –intercepts of a graph? For example: the x intercepts of f(x) = 2x+1

·         Can anyone sketch the graph of f(x) = x2

After thorough discussions of the ideas in the above questions, the teacher could lead students to the discussion of the graphs of quadratic equations starting from thebasic quadratic is y = x2. 

Lesson Notes

The general technique for graphing quadratics is the same as for graphing linear equations. However, since quadratics graph as curvy lines (called "parabolas"), rather than the straight lines generated by linear equations, there are some additional considerations.

incorrect graph

The most basic quadratic function is y = x2. When you graphed straight lines, you only needed two points to graph your line, though you generally plotted three or more points just to be on the safe side. However, three points will almost certainly not be enough points for graphing a quadratic function. For example, suppose a student computes these three points:

 

Then, based only on his experience with linear graphs, he tries to put a straight line through the points. He got the graph wrong.

table of values: (0,0), (1,1), (2,4)

Taking many points:

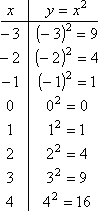
table of values: (-3,9), (-2,4), (-1,1), (0,0), (1,1), (2,4), (3,9), (4,16)

 

The last point has a rather large y-value (16), so we may decide that we won't bother drawing the graph large enough to plot it. Now, plot all the other points:

 

We draw a nicely smooth curving line passing neatly through the plotted points:

plotted points

 

Some students may plot the points correctly, but will then connect the points with straight line segments, like the one in the box. Teacher should remind students the graph must be a smooth curve. They do still need a ruler for doing the graphing, but only for drawing the axes, not for drawing the parabolas. Parabolas graph as smoothly curved lines, not as jointed segments.

incorrect "segment" graph

correct graph of y = x2

Parabolas are smooth curves, not jointed segments like this.

graph of y = x^2

 

 

 

 

The general form y = ax2 + bx + c

For graphing f(x) = ax2 + bx + c, the leading coefficient "a" indicates how "fat" or how "skinny" the parabola will be.

For | a | > 1 (such as a = 3 or a = –4), the parabola will be "skinny", because it grows more quickly (three times as fast or four times as fast, respectively, in the case of our sample values of a).

For | a | < 1 (such as a = 1/3 or a = –1/4), the parabola will be "fat", because it grows more slowly (one-third as fast or one-fourth as fast, respectively, in the examples). Also, if ais negative, then the parabola is upside-down.

We can see these trends when we look at how the curve y = ax2 moves as "a" changes:As the leading coefficient goes from very negative to slightly negative to zero (not really a quadratic) to slightly positive to verypositive, the parabola goes from skinny upside-down to fat upside-down to a straight line (called a "degenerate" parabola) to a fat right-side-up to a skinny right-side-up. Copyright © Elizabeth 2002-2011 All Rights Reserved

There is a simple, if slightly "dumb", way to remember the difference between right-side-up parabolas and upside-down parabolas. If, for instance, you have an equation where a is negative, but you're somehow coming up with plot points that make it look like the quadratic is right-side-up, then you will know that you need to go back and check your work, because something is wrong.

Parabolas always have a lowest point (if the parabola is up side) or a highest point (if the parabola is upside-down). This point, where the parabola changes direction, is called the "vertex".

If the quadratic is written in the form y = a(x – h)2 + k, then the vertex is the point (h, k). This makes sense. The squared part is always positive (for a right-side-up parabola), unless it's zero. So we will always have that fixed value k, and then we will always be adding something to it to make y bigger, unless of course the squared part is zero. So the smallest y can possibly be is y = k, and this smallest value will happen when the squared part, x – h, equals zero. And the squared part is zero when x – h = 0, or when x = h.

The same reasoning works, with k being the largest value and the squared part always subtracting from it, for upside-down parabolas.

Note: The "a" in the vertex form "y = a(x – h)2 + k" of the quadratic is the same as the "a" in the common form of the quadratic equation, "y = ax2 + bx + c".

 

Since the vertex is a useful point, we can complete the square to convert ax2 + bx + c to vertex form, if not written in vertex form, for finding the vertex. But, it's simpler to just use a formula. (The vertex formula is derived from the completing the-square process, just as is the Quadratic Formula. In each case, memorization is probably simpler than completing the square.)

For a given quadratic y = ax2 + bx + c, the vertex (h, k) is found by computing h = , and then evaluating y at h to find k. Since students have already learned the Quadratic Formula, they may find it easy to memorize the formula for k. It is related to both the formula for h and the discriminate in the Quadratic Formula: k= .

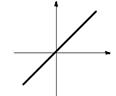
Example: Find the vertex of y = 3x2 + x – 2 and graph the parabola.

To find the vertex, we look at the coefficients a, b, and c. The formula for the vertex gives me:

h = –b/2a = –(1)/2(3) = –1/6

Then we can find k by evaluating y at h = –1/6:

k = 3( –1/6 )2 + ( –1/6 ) – 2

= 3/36 – 1/6 – 2

= 1/12 – 2/12 – 24/12

= –25/12

So, we know that the vertex is at (–1/6 , –25/12 ). Using the formula was helpful, because this point is not one that we were likely to get on the T-chart. We need additional points for our graph:

T-chart: (-2,8), (-1,0), (0,-2), (1,2), (2,12)

 

Now we can draw the graph, and we will label the vertex:

graph of y = 3x^2 + x - 2, with vertex marked and labelled

 

The only other consideration regarding the vertex is the "axis of symmetry". If we look at a parabola, we will notice that we could draw a vertical line right up through the middle which would split the parabola into two mirrored halves. This vertical line, right through the vertex, is called the axis of symmetry. If we are asked to determine the axis, we simply write down the line "x = h", where h is just the x-coordinate of the vertex. So in the example above, then the axis would be the vertical line x = h = –1/6.

Note: If the quadratic function has x-intercepts, a shortcut for finding the axis of symmetry is to note that this vertical line is always exactly between the two x-intercepts. So we can just take the average of the two intercepts to get the location of the axis of symmetry and the x-coordinate of the vertex.

Example:  Find the vertex and intercepts of y = 3x2 + x – 2 and graph; remember to label the vertex and the axis of symmetry.

Solution: We can find the vertex easily using the formula. But, we shall find the intercepts before we draw the graph. To find the y-intercept, we set x equal to zero and solve:

y = 3(0)2 + (0) – 2 = 0 + 0 – 2 = –2

Then the y-intercept is the point (0, –2). To find the x-intercept, we set y equal to zero, and solve:

0 = 3x2 + x – 2
0 = (3x – 2)(x + 1)
3x – 2 = 0 or x + 1 = 0
x = 2/3 or x = – 1

Then the x-intercepts are at the points (–1, 0) and ( 2/3, 0).

The axis of symmetry is halfway between the two x-intercepts at (–1, 0) and at ( 2/3 , 0); using this, we can confirm the answer from the previous page:

(–1 + 2/3) / 2 = (–1/3) / 2 = –1/6

The complete answer is a listing of the vertex, the axis of symmetry, and all three intercepts, along with a nice neat graph:

The vertex is at ( –1/6 , –25/12 ), the axis of symmetry is the line x = –1/6 , and the intercepts are at (0, –2), (–1, 0), and ( 2/3, 0).

graph of y = 3x^2 + x - 2 with vertex and intercepts marked.

Example: Find the intercepts, the axis of symmetry, and vertex of y = x2 – x – 12.

Solution: To find the y-intercept, we set x equal to 0 and solve:

y = (0)2 – (0) – 12 = 0 – 0 – 12 = –12

To find the x-intercept, we set y equal to 0 and solve:

0 = x2 – x – 12

0 = (x – 4)(x + 3)

x = 4 or x = –3

To find the vertex, we look at the coefficients: a = 1 and b = –1. Inserting into the formula, we get:

h = –(–1)/2(1) = 1/2 = 0.5

To find k, we replace h = 1/2 for x in y = x2 – x – 12, and simplify:

k = (1/2)2 – (1/2) – 12 = 1/4 – 1/2 – 12 = –12.25

Once we have the vertex, it's easy to write down the axis of symmetry: x = 0.5. Now, we will find some additional plot points, to fill in the graph:

T-chart    graph of y = x^2 - x - 12

For convenience, we may pick x-values that were centered on the x-coordinate of the vertex. Now we can plot the parabola as shown above and the final answer to our questions are:

·         The vertex is at the point (0.5, –12.25),

·         The axis of symmetry is the line x = 0.5,

·         The intercepts are at the points (0, –12), (–3, 0), and (4, 0).

 

Example: Find the x-intercepts and vertex of y = –x2 – 4x + 2.

Solution:

Since it is so simple to find the y-intercept, they are only asking for the x-intercepts this time. To find the x-intercept, we set y equal 0 and solve:

0 = –x2 – 4x + 2

x2 + 4x – 2 = 0

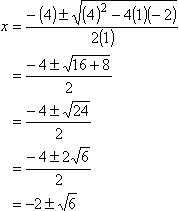
x = -2 ± sqrt(6)

To find the vertex, we look at the coefficients: a = –1 and b = –4. Then:

h =  = –2

To find k, we replace h = –2 in for x in y = –x2 – 4x + 2, and simplify:

k = –(–2)2 – 4(–2) + 2 = –4 + 8 + 2 = 10 – 4 = 6

Now we will find some additional plot points, to help us sketch the graph:

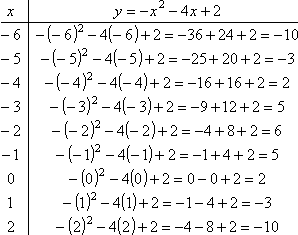
T-chart  graph of y = -x^2 - 4x + 2

Note that we picked x-values that were centered on the x-coordinate of the vertex. Thus,

·         The vertex is at (–2, 6),

·         The x intercepts are points: ) and  )

Example:  Find the x-intercepts and vertex of y = –x2 + 2x – 4.

To find the vertex, I look at the coefficients: a = –1 and b = 2. Then:

h =  = 1

To find k, replace h= 1 for x and simplify:

k = –(1)2 + 2(1) – 4 = –1 + 2 – 4 = 2 – 5 = –3

The vertex is below the x-axis, and, since the leading coefficient is negative, the parabola is going to be upside-down. So can the graph possibly cross the x-axis? Can there possibly be any x-intercepts? Of course not! So we expect to get "no (real) solution" when we try to find the x-intercepts, but we shall show the work anyway. To find the x-intercept, we set y equal 0 and solve:

0 = –x2 + 2x – 4

x2 – 2x + 4 = 0

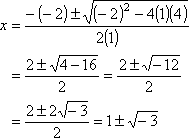
x = 1 ± sqrt(-3), wihich is not real.

As soon as we get a negative inside the square root, we know that we can't get a solution. So, as expected, there are no x-intercepts. Now, let’s find some additional plot points, to draw the graph:

T-chart  graph of y = -x^2 + 2x - 4

Therefore, the vertex is at (1, –3), and the only intercept is y intercept at (0, –4).

Concluding Activities

The teacher shall make sure that the following summary points of the topic are well taken by the students. The teacher could use a short quiz or a test to evaluate students’ progress apart from observation while guiding the practice.

·         The graph of a quadratic function,f(x) = ax2 + bx + c, a Ή 0,is a parabola which turns up if a > 0 and down if a < 0.

·         The turning point of the graph of a quadratic function     f(x) = ax2 + bx + c, a Ή 0 is called the vertex. It can be obtained from

·         The vertical line through the vertex(turning point) is called the axis of symmetry. It is the vertical line

·         Any quadratic function f(x) = ax2+bx+c, a Ή 0 can be written as f(x) = a(x+d)2 + e using completing the square method.

 

Practice Exercises

1.      Rewrite f(x) = x2 + 2x - 24 in the form f(x) = (x+d)2 +e, where   d, e, ΞR. Indicate the vertex & sketch the graph.

2.      Rewrite f(x) = 2x2 – 3x – 6 in the form f(x) = a(x+d)2 + e and find the vertex.

3.      What do we do to get the graphs of the following from the graph of f(x) = x2.

                    i.            g(x) = x2 + 5

                  ii.            g(x) = x2 – 5

                iii.            g(x) = (x – 5)2

                   iv.            g(x) = (x + 5)2

4.  Determine the intercepts, vertex and axis of symmetry for each of the following quadratic functions and then sketch their graphs.

                    i.            f(x) = -3x2

                  ii.            f(x) = -x2 – 5

                iii.            f(x) = -x2 + 5