Unit 4: Topic 3: Domain and Range of Functions

Competencies

· Determine the domain of functions

· Determine the range of functions

Methods of Teaching the Topic: Group discussion including guided practice

Starter Activities

Focus and Review: The teacher shall remind students what has been learned in previous lessons that will be pertinent to this lesson and/or have them begin to think about the words and ideas of this lesson. Ask the students if they remember:

· What relations are and what functions are.

· The meaning of domain and range of relations

· The definition of functions

· To identify a given graph represents a function or not

· The vertical line test and what it is used for

Expected Explanations

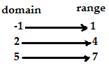
A "relation" is just a relationship between sets of information. Think of all the people in one of your classes, and think of their heights. The pairing of names and heights is a relation. In relations and functions, the pairs of names and heights are "ordered", which means one comes first and the other comes second. To put it another way, we could set up this pairing so that you give me a name, and then I give you that person's height, or else you give me a height, and I give you the names of all the people who are that tall. The set of all the starting points is called "the domain" and the set of all the ending points is called "the range." The domain is what you start with; the range is what you end up with. The domain is the x's; the range is the y's.

A function is a "well-behaved" relation. Just as with members of your own family, some members of the family of pairing relationships are better behaved than other. This means that, while all functions are relations. But, not all relations are functions. When we say that a function is "a well-behaved relation", we mean that, given a starting point, we know exactly where to go; given an x, we get only and exactly one y. The teacher may use the following examples to explain what function means.

2	This is a function. You can tell by tracing from each x to each y. There is only one y for each x; there is only one arrow coming from each x.
	This is a function! There is only one arrow coming from each x; there is only one y for each x. It just so happens that it's always the same y for each x, but it is only that one y. So this is a function; it's just an extremely boring function!
	This one is not a function: there are two arrows coming from the number 1; the number 1 is associated with two different range elements. So this is a relation, but it is not a function.
	Okay, this one's a trick question. Each element of the domain that has a pair in the range is nicely well-behaved. But what about that 16? It is in the domain, but it has no range element that corresponds to it! This won't work! So then this is not a function. It is not even a relation!
	This one is straight forward. For one domain element we have only one range element and vice-versa. It is a one to one function.

The "Vertical Line Test"

To continue with the discussion on functions graphically, the teacher might pause questions of the following type to be answered by a small group discussion: “what if we sketch the graph of the relation that consists of a set containing just two points: {(2, 3), (2, –2)} and test it with the vertical line test?” We already know that this is not a function, since x = 2 goes to each of y = 3 and y = –2.

If we graph this relation, it looks like:
Notice that you can draw a vertical line through the two points, like this:

This characteristic of non-functions was noticed and was codified in "The Vertical Line Test": Given the graph of a relation, if you can draw a vertical line that crosses the graph in more than one place, then the relation is not a function. Here are a couple examples:

	This graph shows a function, because there is no vertical line that will cross this graph twice.
	This graph does not show a function, because any number of vertical lines will intersect this oval twice. For instance, the y-axis intersects (crosses) the oval curve twice.

Lesson Notes

"Is it a function?" - Quick answer without the graph

Think of all the graphing that you've done so far. The simplest method is to solve for "y =", make a T-chart (table of values), pick some values for x, solve for the corresponding values of y, plot your points, and connect the dots. Not only is this useful for graphing, but this methodology gives yet another way of identifying functions: If you can solve for "y =", then it's a function. For example, 2y + 3x = 6 is a function, because you can solve for y:

2y + 3x = 6
2y = –3x + 6
y = x + 3

On the other hand, y² + 3x = 6 is not a function, because you can’t solve for a uniquey:

y² + 3x = 6

y²= – 3x + 6

y =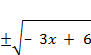

This is solved for "y =", but it's not unique. Do we take the positive square root, or the negative? So, in this case, the relation is not a function. (We can also check this by using our first definition from above. Think of "x = –1". Then, we get y² – 3 = 6, so y² = 9, and then y can be either –3 or +3. That is, if we did an arrow chart, there would be two arrows coming from x = –1.)

Functions: Domain and Range

Let's return to the discussion of domains and ranges. When functions are first introduced, you will probably have some simplistic "functions" and relations to deal with, being just sets of points. These won't be terribly useful or interesting functions and relations, but your text wants you to get the idea of what the domain and range of a function are. For instance:

· State the domain and range of the following relation. Is the relation a function?
{(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}

The above list of points, being a relationship between certain x's and certain y's, is a relation. The domain is all the x-values, and the range is all the y-values. To give the domain and the range, we just list the values without duplication:

Domain: {2, 3, 4, 6} and Range: {–3, –1, 3, 6}

Students could be reminded that it is customary to list these values in numerical order, but it is not required. Sets are called "unordered lists", so they can list the numbers in any order they feel like. Just should not duplicate.

While the given set does represent a relation (because x's and y's are being related to each other), they give two points with the same x-value: (2, –3) and (2, 3). Since x = 2 gives two possible destinations, then this relation is not a function.

Note that all we had to do to check whether the relation is a function, is to look for duplicate x-values. If we find a duplicate x-value, then the different y-values mean that we do not have a function.

Example:

Given the relation:{(–3, 5), (–2, 5), (–1, 5), (0, 5), (1, 5), (2, 5)}, state the domain and range of the following relation. Is the relation a function?

Just list the x-values for the domain and the y-values for the range: So,

Domain: {–3, –2, –1, 0, 1, 2} and Range: {5}

In this example, every x-value goes to the exact same y-value. But each x-value is different, although it is boring; this relation is indeed a function. In point of fact, these points lie on the horizontal line y = 5.

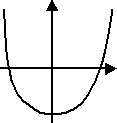
Example: Is the following graph a function or not? If it is, write its domain and range.

Solution: It passes the vertical line test and so it is a function.

As the graph moves non- stop downward, its domain = R (all real numbers) and the Range is {y: y } = (-¥, 1]

Example: Determine the domain and range of the following functions from their equations

a) f(x) = |x – 1|

b) f (x) = x² – 4x + 3

Solution:

a) f (x) = |x – 1|

All real numbers can fit into the value of x. Thus, Domain = R

But, for any value of x, the result y is always greater than or equal to 0. Thus, Range = {y: y [0, ¥)

b) f (x) = x² – 4x + 3 Þ using completing the square method, f(x) = (x – 2)²– 1

Domain = R Range = [-1, ¥)

The possible values of x is x < 1 in the first part and x . Thus, the union is the set of all real numbers. So, Domain = R. For any real number x, the maximum we get is 2. Thus, Range = (-¥, 2]

Domain of Composed functions: Sometimes some functions might be combinations of other functions. In that case the domain of such functions can be obtained by taking the intersection of the domains of the parts.

Example: Find the domain of h(x) = + x² – 1.

Solution: h(x) = + x² – 1 can be sum of two functions. f(x) = and g(x) = x² – 1

Domain of f = [0, ¥) and Domain of g = R

Domain of h(x) = Domain of (f + g) (x) = Domain of fÇ Domain of g

= [0, ¥ ) ÇR = [0, ¥ )

Example: Find the domain of f(x) = +.

Solution:

f(x) = + can be expressed as a sum of two functions g(x) = and r(x) =

Domain of g = x ³ - 4 or [-4, ¥)

Domain of r = R\ {-4}

Domain of f(x) = Domain of (g +r) (x) = [-4, ¥)ÇR\ {-4}

= (-4, ¥)

Concluding Activities

The teacher shall make sure that the following are summarized by the students through exercises.

A Relation R is a function if and only if whenever (x, y) Î R and (x, z) Î R then y = z.
If a vertical line touches the graph of a relation at not more than one place, then the graph represents a function.
The domain of the sum, difference, product and quotient of the two functions can be obtained from (Dom f) Ç (Dom of g)

Practice Exercises

1. Determine the domain and range of the following functions

A. f(x) = |x|

B. f(x) = x^z

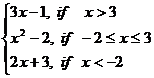
C. f(x) =