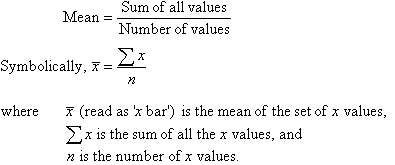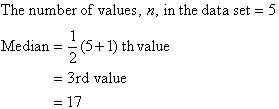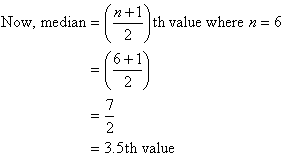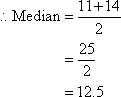Topic 1: Variance and Standard Deviation

Competencies

·   Determine the variance of a given statistical data

·   Find the standard deviation of a given data

Suggested ways of teaching this topic: Q &A and Guided Discovery

Starter Activities

The teacher could start with the revision of previous lessons on the measures of Central Tendency – Mean, Median and Mode using Q & A, asking questions like:

·         What is statistics?

·         What do we mean by population? Sample?

·         What are the measures of Central Tendency?

·         How can we find each measure of central Tendency? Show the steps using examples.

Expected Replies

A population is the whole set of items from which a data sample can be drawn; so a sample is only a portion of the population data. Features of a sample are described by statistics.

Statistical methods enable us to arrange, analyze and interpret the sample data obtained from a population. We gather sample data when it is impractical to analyze the population data as a smaller sample often allows us to gain a better understanding of the population without doing too much work or wasting precious time. Measures of Central Tendency We make inferences about a population from a sample set of observed values by finding the mean, median and mode. The mean, median and mode are collectively known as measures of central tendency Mean The mean (or average) of a set of values is defined as the sum of all the values divided by the number of values. That is: Example: The marks of five candidates in a mathematics test with a maximum possible mark of 20 are given below: 14;      12;   18;     17;     13. Find the mean value. Solution: So, the mean mark = is 14.8 Median The median is the middle value of the data set arranged in ascending order of magnitude. Example: The marks of five candidates in a geography test for which the maximum possible mark was 20 are given below: 18;17;15;14;19 Find the median mark. Solution: Arrange the marks in ascending order of magnitude: 14, 15, 17, 18, 19 The third value, 17, is the middle one in this arrangement. So, median = 17 Note: In general: If the number of values in the data set is even, then the median is the average of the two middle values. Example:  Find the median of the following scores: 10 16 14 19 8 11 Solution: Arrange the values in ascending order of magnitude: 8, 10, 11, 14, 16, 19 There are 6 values in the data set. Therefore n = 6 The third and fourth values, 11 and 14, are in the middle. That is, there is no one middle value. Note: Half of the values in the data set lie below the median and half lie above the median. Mode The mode is the value (or values) that occur most often. Example: The marks awarded to seven pupils for an assignment were as follows: 18; 14; 18; 15; 12; 19; 18 A.    Find the median mark. B.     State the mode. Solution: a)      Arrange the marks in ascending order of magnitude:  12, 14, 15, 18 ,18, 18, 19 Note: The fourth mark, 18, is the middle data value in this arrangement. b)      18 is the mark that occurs most often (It is repeated 3 times). After a complete revision of the measures of central tendency, especially, how to determine the mean, the discussions on Variance and Standard Deviation shall continue using guided discovery method, where the teacher leads the students towards the formulae. Lesson Notes

Standard Deviation and Variance

The variance and the closely-related standard deviation are measures of how spread out a distribution is. In other words, they are measures of variability or dispersion.
The variance is computed as the average squared deviation of each number from its mean. For example, for the numbers 1, 2, and 3, the mean is 2 and the variance is:

.

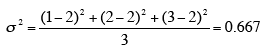The formula (in summation notation) for the variance in a population is

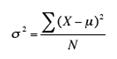Where μ is the mean and N is the number of scores.

When the variance is computed in a sample, the statistic
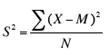(where M is the mean of the sample) can be used. S² is a biased estimate of σ².

However, by far the most common formula for computing variance in a sample is:
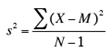which gives an unbiased estimate of σ².

Since samples are usually used to estimate parameters, s² is the most commonly used measure of variance. Calculating the variance is an important part of many statistical applications and analyses. It is the first step in calculating the standard deviation.

Standard Deviation

The standard deviation formula is very simple: it is the square root of the variance. It is the most commonly used measure of spread. The standard deviation has proven to be an extremely useful measure of spread in part because it is mathematically controllable. Many formulas in inferential statistics use the standard deviation.

Example: Find the variance and standard deviation, to one decimal place, of population function whose distribution is given below.

Values	1      3       5      7      9
Frequency	2      3       2      3      2

Solution:

Step 1)    = = = 5

	Value	1	3	5	7	9
Step 2)	xi  -	1-5	3-5	5-5	7-5	9-5
Step 3)	( xi  -)2	(-4)2	(-2)2	(0)2	(2)2	(4)2
	Frequency	2	3	2	3	2
Step 4)	fi ( xi  -)2	2(-4)2	3(-2)2	2(0)2	3(2)2	2(4)2

 

 

 

 

 Step 5) Variance = d² =

                          =

Step 6) Standard deviation = d = » 2.7

Example:Find the variance and standard deviation to one decimal place, of the population function whose distribution is given below.

Values	1      2       3      4      5
Frequency	3      3       1      1      4

 

 

Solution:

Step 1)     = = = = 3

	Value	1	2	3	4	5
Step 2)	xi -	1-3	2-3	3 - 3	4 - 3	5-3
Step 3)	(xi -)2	(-2)2	(-1)2	(0)2	(1)2	(2)2
	Frequency	3	3	1	1	4
Step 4)	fi (xi -)2	3 (-2)2	3(-1)2	1(0)2	1(1)2	4(2)2

 

 

 

 

 

 Step 5)    Variance = d² =

= 2.7

Step 6) The standard deviation

d = » 1.6 to one decimal place.

Practice Exercises

1.      For the numbers 1, 2, 4, 4, 5, 8; find

i)              their mean, median and mode

ii)            the range, variance and standard deviation

2.      Given the following distribution table, find

i)        the measures of central tendency

ii)      the measures of dispersion

iii)    the histogram that represents the distribution

v	2	4	6	7	10
f	6	2	3	6	1

3.      Use the given histogram to find the mean, median, mode, range, mean deviation, variance and standard deviation of the population function.