Unit 3: Sets
Topic 1: Venn Diagrams and Sets
Competencies
· Describe the
terminology used with sets and Venn diagrams.
· Determine the
placement of an element in a Venn diagram.
· Apply the notion
of Venn diagrams to solve problems related to sets.
Suggested
ways of teaching this topic: teacher explanation, guided practice and
individual practice
Starter
Activities
The teacher may lead the students in a short discussion about Venn Diagrams. This topic is where we introduce the ideas of sets and Venn diagrams. A set is a list of objects in no particular order; they could be numbers, letters or even words. A Venn diagram is a way of representing sets visually.
Teacher
explanation and input
To explain, the
teacher could start with an example where we use whole numbers from 1 to 10.
We will define two sets taken from this group of numbers:
Set A = the odd
numbers in the group = { 1 , 3 , 5 , 7 , 9 }
Set B = the numbers which are 6 or more in the group = { 6 , 7 , 8 , 9 , 10 }
Some numbers from
our original group appear in both of these sets. Some only appear in one of the
sets.
Some of the original numbers don't appear in either of the two sets. We can
represent these facts using a Venn diagram.

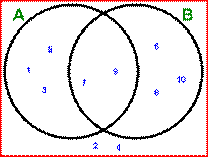
The
two large circles represent the two sets.
The numbers which appear in both
sets are 7 and 9. These will go in the central section, because this is part of
both circles.
The numbers 1, 3 and 5 still
need to be put in Set A, but not in Set B, so these go in the left section of
the diagram.
Similarly, the numbers 6, 8
and 10 are in Set B, but not in Set A, so these will go in the right section of
the diagram.
The numbers 2 and 4 are not
in either set, so will go outside the two circles.
The
final Venn diagram looks like this:
We can see that all ten original numbers appear in the diagram.
The numbers in
the left circle are Set A
{ 1 , 3 , 5 , 7 , 9 }
The numbers in
the right circle are Set B
{ 6 , 7 , 8 , 9 , 10 }
Guided
Practice
After students understood the basic ideas, the rest of the lesson will be student’s practice filling in Venn diagrams and using them.
Lesson Notes
|
|
The
intersection of sets A and B is those elements which are in set Aandset B.
A diagram showing the intersection of A and B is on the left. The union of sets A and B is those elements which are in set Aorset Borboth. A diagram showing the union of A and B is on the right. |
|
Setting: Ten Best Friends
The teacher could take a set made up of ten best friends listing them like:
{Alemu, Balcha, Kassa, Demis, Eshet, Fire, Genet, Hadush, Imam, Jasmin}
Each friend is an "element" (or "member") of the set
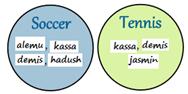
Now let's say that alemu, kassa, demis and hadush play Soccerand kassa, demis and jasmin play Tennis. That is,
"Soccer" = {Alemu, Kassa, Demis, Hadush}
Tennis = {Kassa, Demis, Jasmin}
You could put their names in two separate circles:
Union
You can now list your friends that play Soccer OR Tennis. Not everyone is in that set. Only your friends that play Soccer or Tennis.
This is called a "Union" of sets and has the special symbol ∪:
Soccer ∪ Tennis = {Alemu, Kassa, Demis, Hadush, Jasmin}
We can also put it in a "Venn Diagram":
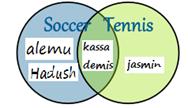
A Venn diagram is better because it shows lots of information easily.
- Do you see
that Alemu, Kassa, Demis and Hadush are in the
"Soccer" set?
- And that Kassa, Demis and Jasmin are in the "Tennis" set?
- And here is
the clever thing: Kassa and Demis are in BOTH sets!
Intersection
"Intersection" is those who are in BOTH sets.
In this we mean those who they play both Soccer AND Tennis ... which is Kassa and Demis.
The special symbol for Intersection is an upside down "U" like this: ∩
And this is how we write it down:
Soccer ∩ Tennis = {Kassa, Demis}
In a Venn diagram, it looks as follows:

Difference
You can also "subtract" one set from another.
For example, taking Soccer and subtracting Tennis means people that play Soccer but NOT Tennis ... which is Alemu and Hadush.
And this is how we write it down:
Soccer - Tennis = {Alemu, Hadush}
In a Venn diagram, difference of two sets can be seen as follows:

Summary So Far
- ∪ is Union: is in either set
- ∩ is Intersection: must be in
both sets
- - or \ is
Difference: in one set but not the other
Three Sets
You can also use Venn Diagrams for 3 sets.
Let us say the third set is "Volleyball", which Demis, Genet and Jasmin play:
Volleyball = {Demis, Genet, Jasmin}
But let's be more "mathematical" and use a Capital Letter for each set:
- S means the set of Soccer
players
- T means the set of Tennis
players
- V means the set of Volleyball
players
The Venn diagram Union of 3 Sets: S ∪ T ∪ V is now like this:
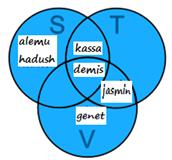
You can see (for example) that:
- Demis plays Soccer, Tennis and
Volleyball
- Jasmin plays Tennis and Volleyball
- Alemu and Hadush
play Soccer, but don't play Tennis or Volleyball
- no-one
plays only Tennis
We can now have some discussions on Venn diagrams of Unions and Intersections.
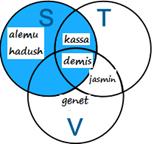
This is just the set S
S = {Alemu, Kassa, Demis, Hadush}
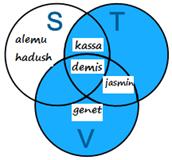
This is the Union of Sets T and V
T ∪ V = {Kassa, Demis, Jasmin, Genet}
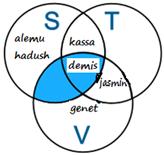
The shaded part shows the Intersection of Sets S and V. (only Demis is available)
Thus, S ∩ V = {Demis}
The teacher may ask students as: “how about performing the following?”
- take the previous
set S ∩ V
- then subtract
T:
Expected Answer
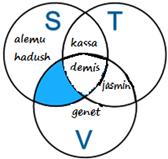
This is the Intersection of Sets S and V minus Set T
(S ∩ V) - T = {}
Look, there is nothing there!
That is just the "Empty Set". It is a null set, so we use the curly brackets with nothing inside: {}
Universal Set
The Universal Set is the set that contains Everything that we are interested in the discussion.
Sadly, the symbol is the letter "U" ... which is easy to confuse with the ∪ for Union. Students must be reminded to be careful not to mix up the symbols.
In our case the Universal Set is our Ten Best Friends.
U = {Alemu, Balcha, Kassa, Demis, Eshet, Fire, Genet, Hadush, Imam, Jasmin}
We can show the Universal Set in a Venn diagram by putting a box around the whole thing:

Now you can see ALL your ten best friends, neatly sorted into what sport they play (or not!).
And then we can do interesting things like take the whole set and subtract the ones who play Soccer:

We write it this way:
U –S = {Balcha, Eshet, Fire, Genet, Imam, Jasmin}
U – S means: "The Universal Set minus the Soccer Set is the Set {Balcha, Eshet, Fire, Genet, Imam, Jasmin}". In other words, U – S is: "everyone who does not play Soccer".
Independent
practice
o
Allow
the students to work by themselves and to complete a worksheet, the teachershould prepare and provide one. Monitor them for
questions and to be sure that the students are working
o
Students
may need help with some of the later questions. Not all of the Venn diagram
questions are math related. Some relate to science, and some to common
knowledge, in order to allow students to practice Venn diagrams more fully. Thus,
teacher shall help the class to talk about what an unknown word could
be--chances are good that if one student does not know what a word means,
someone else in the class will.
|
Example 1:Given the following Venn diagram, answer each of the following questions (a)
Which numbers are in the union
of A and B? Solution: (a) A (b) A |
|
Example
2: For any two
non-empty sets A and B, Use Venn diagrams to show that:
a) (A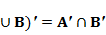 b) (A
b) (A 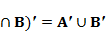
Solution:

Looking
at the following Venn diagram,
a) A![]() can be seen on regions I, II and III
can be seen on regions I, II and III
So, (A![]() is seen in region IV
is seen in region IV
On
the other hand, A![]() is covered by regions III and IV, while B
is covered by regions III and IV, while B![]() is covered by regions I and IV.
is covered by regions I and IV.
So,![]() is region IV. This shows that(A
is region IV. This shows that(A![]() are represented by the same region, IV.
are represented by the same region, IV.
Thus,(A![]()
b)
A![]() is seen on region II
is seen on region II
So,(A![]() is seen in regions I, III and IV
is seen in regions I, III and IV
On
the other hand, A![]() is covered by regions III and IV, while B
is covered by regions III and IV, while B![]() is covered by regions I and IV.
is covered by regions I and IV.
So,![]() is represented by regionsI, III andIV. This shows that(A
is represented by regionsI, III andIV. This shows that(A![]() are represented by the same region, IV.
are represented by the same region, IV.
Thus,(A![]()