Unit 2: Topic 6: Application
of Viete’s Theorem
Competencies
·
State
Viete’s theorem
·
Apply
Viete’s theorem to solve problems
Suggested ways
of teaching this topic: Presentation of the teacher followed by individual
consolidation and practice activities
Starter
Activities
Before coming to the discussion on Viete’s theorem and its application, the students shall
understand the nature of the roots of a quadratic equation. The teacher might
start from “A Question and Answer Session” where students can be asked to solve
the following quadratic equation and find out the relationship between the
roots and the coefficients of the equation. The process goes as follows:
Example:
Solve
each of the following equations by using the quadratic formula:
a)
2x2
– 3x – 2 = 0
b)
4x2
– 4x + 1 = 0
c)
3x2
– 2x + 1 = 0
Solution:
a) 2x2 –
3x – 2 = 0
̃ a = 2, b = -3,
c = -2

![]()
![]() or
or
![]()
![]()
b) 4x2 –
4x + 1 = 0
̃ a = 4, b = - 4,
c = 1
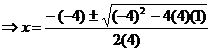
![]() =
=
![]() =
= ![]()
c) 3x2 –
2x + 1 = 0
̃ a = 3, b = -2,
c = 1

![]()
![]()
Since![]() , where a>
0, is undefined; this equation has no
solution.
, where a>
0, is undefined; this equation has no
solution.
At
this stage, the teacher shall ask students to observe the value of b2 - 4ac (the expression
inside the square root)for each of the three
quadratics. The expected results are:
For a); b2
- 4ac = 25, which is greater than 0
For b); b2
- 4ac = 0
For c); b2 - 4ac = - 8, which is less than
zero.
The
next is asking an important question: “What
do you observe from the sign of b2 – 4ac and the number solutions of
these equations?”
Expected Answer
·
From
the examples solved above, it is clear that the expression b2 - 4ac
is the key to determine the nature of roots of a given quadratic equation.
·
The
expression b2 - 4ac is called the discriminate and its value will
enable us to make predictions regarding the types of roots that we will obtain.
Lesson Notes
Let
D = b2 – 4ac.
1.
If
D > 0, then the equation ha 2 distinct solution
2.
If
D = 0, then the equation has exactly 1 solution
3.
If
D < 0, then the equation has No solution
Example:
Find the discriminate of the following
equations and determine their nature of roots, without actually
solving any of them:
a)
x2
+ 2x – 5 = 0
b)
2x2
– x + 1 = 0
c)
x2
+ 5x – 6 = 0
d)
x2
+ 4x +4 = 0
Solution:
a) x2 + 2x – 5 = 0
̃
a= 1, b= 2, c = -5
̃ D = b2
– 4ac = 22 – (4)(1)(-5) = 24
D > 0 ̃ 2 distinct
Solution
b) 2x2 –
x + 1 = 0
̃
a = 2, b = -1, c= 1
̃ D=b2–4ac=(-1)2 (0) - (4)(2)(1) = -7
D < 0 ̃ No solution
c) x2 +
5x – 6 = 0
̃
a = 1, b = 5, c = -6
̃ D = b2
– 4ac = 52 – 4(1)(-6) = 25 + 24 = 49
D > 0 ̃ two distinct
solutions
d) x2 +
4x +4 = 0
̃
a = 1, b = 4, c = 4
̃ D = b2
– 4ac = 42 – 4(1)(4)
= 16 – 16 = 0
D = 0 ̃ Exactly 1
solution
Applications of the Nature of Roots
Example
1:
For which values of k will the equation 2x2+kx
+ 1 = 0 have equal roots?
Solution: a = 2, b = k and
c = 1
̃ D = b2
– 4ac = (k)2 -4(2)(1)
= k2
– 8
But D = 0 (equal roots)
̃ k2 –
8 = 0
̃ k = ±![]()
Example
2:
Find the value of k for which the
quadratic equationx2 - 8x + k =0 will have exactly one solution.
Solution: a = 1, b= -8, c
= k
̃ D = b2
– 4ac = (-8)2 – 4(1)(k) = 64 – 4k
But D = 0 (which means one
solution)
̃ 64 – 4k = 0
̃ 64 = 4k
̃ k = 16
Example
3:
Find the value(s) of k for which the
quadratic equation 3x2 -2kx + 3 = 0 will have exactly one solution.
Solution:
3x2 – 2kx + 3 = 0
̃ a = 3, b = -2k,
c = 3
̃ D = b2
– 4ac = (-2k)2 – 4(3)(3)
= 4k2 – 36
But D = 0 ̃ 4k2
= 36
̃ k = ± 3
Now,
before stating the theorem, the teacher could take one of the quadratic
equations with two roots and ask students to
1.
add
the roots, then compare the sum with the value of ![]() for that equation
for that equation
2.
multiply
the roots , then compare the product with the value of ![]() for that equation
for that equation
If x2 + 5x – 6 = 0
were taken the roots are r1 = - 6 and r2 = 1.
Thus, r1 + r2 =
- 6 + 1 = -5 = ![]() and r1
and r1![]() r2 = - 6
r2 = - 6 ![]() 1 = - 6 =
1 = - 6 =
![]()
This
is time the theorem that explains the existing special relationship between the
roots of a quadratic equation and its coefficients can be stated.
Viete’s Theorem
Theorem: If the root of ax2 + bx + c = 0, a≠0 are r1 and r2,
then
a)
![]()
b)
![]()
Example 4: Check Viete’s theorem using2x2+ 3x – 5 = 0
̃ a = 2, b = 3, c
= -5
Checking
Viete’s Theorem:
Sum: ![]()
Product:
![]()
Example 5: Without computing the roots a and b of the equation
3x2 + 2x + 6 = 0 find
1.
a+ b
2.
ab
3.
![]()
Solution:
From
3x2 + 2x + 6 = 0, a = 3, b = 2, c = 6
1) a + b= ![]()
2) ab = ![]()
![]()
̃
Example 6: Without computing the roots a and b of the equation
2x2 – 5x – 12 = 0, find
a) ![]()
b) ![]()
Solutions:
2x2
– 5x – 12 = 0 ̃ a = 2, b = -5
, c = -12
a) ![]() =
= ![]()
![]()
b) ![]()
![]()
= ![]()
![]()
![]()
Practice
Exercises
1.
Find
the discriminate for each of the listed equations and determine their nature of roots, without actually
solving any of the equations:
a) 2x2 –
5x + 3 = 0
b) 9x2 +
x + 1 = 0
c) 4x2 +
4x + 1 = 0
d) x2 –
5x – 3 = 0
2.
How
many solutions does each equation have?
a)
3x2
– x + 2 = 0
b)
2x
– x2 + 15 = 0
c)
1
– 2x + x2 = 0
3.
If
one of the roots and the product of the roots of the equation 6x2 + Mx + N = 0 respectively are ½ and -2/3 ,
what are the values of M and N?
4.
For
what value of k will (k+3)x2 + (3k+1)x + 1
= 0 have only one root?
5.
A
quadratic equation has two unequal roots. If the difference between them is 1
and the difference of their squares is 2, what will be the equation?
For the
following questions choose the best answer
1. Which one of the
following equations has two distinct roots?
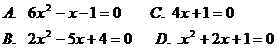
2. Which one gives
the sum of the roots of the quadratic equation ![]() ?
?
![]()
3. If -2 and 3 are
the roots of ![]() then what are the values of M and N respectively?
then what are the values of M and N respectively?
![]()
5. If one root of ![]() is 5, for some constant
is 5, for some constant ![]() , then the other solution is:
, then the other solution is:
A.
-25
B.
25
C.
-5
D.
5
6. If ![]() is a constant number and
is a constant number and ![]() has at most
one real root, then what is the minimum value of
has at most
one real root, then what is the minimum value of![]() ?
?
![]()
7. The set of values of ![]() for which
for which ![]() has only one
root is:
has only one
root is:
![]()
8. If one of the roots of the equation ![]() exceeds the
other by 4 then k is equal to:
exceeds the
other by 4 then k is equal to:
A.
12
B.
15
C.
16
D.
6