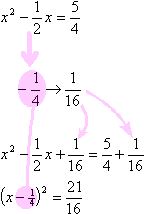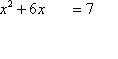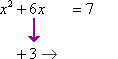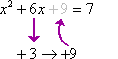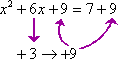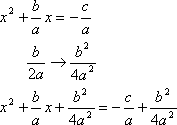Unit 2: Topic 5: Solving
Quadratic Equations using Completing the Square
Competencies
·
Perform
completing square
·
Solving
quadratic equations using completing the square
Suggested ways
of teaching this topic: Jigsaw in small groups
Starter
Activities
The teacher might start with
some quadratic equations which are fairly simple to solve like those of the
form "something-with-x squared equals some number", and then with
trinomials. An example would be:
(x 4)2 = 5
x 4 = ±![]()
x = 4 ± ![]()
x = 4 ![]() and x = 4
+
and x = 4
+ ![]()
Unfortunately, most
quadratic equations don't come neatly squared like this. Thus, students shall
learn how to use the technique of "completing the square" to
rearrange the quadratic into the neat "(squared part) equals (a
number)" format demonstrated above.
The teacher can demonstrate
the steps using one of the following examples. Then, the teacher can prepare
similar questions and give each group one question. Let students work in their
groups for some time and then disperse the home group and form other groups
where each student can share other groups solutions.
Lesson
Notes
Example 1: Solve the equation: 4x2 2x 5=0.
Solution:
|
This is the original problem. |
4x2 2x
5 = 0 |
|
Move the loose number over to the other side. |
4x2 2x
= 5 |
|
Divide through by whatever is multiplied on the squared term. Take half of the coefficient (don't forget the sign!) of the x-term,
and square it. Add this square to both sides of the equation. Convert the left-hand side to squared form, and simplify the
right-hand side. (This is where you use that sign that you kept track of
earlier. You plug it into the middle of the parenthetical part.) |
|
|
Taking the square root both sides, remembering the "±"
on the right-hand side. Simplify as necessary. |
|
|
Solve for "x =". |
|
|
Remember that the "±" means that you have two values
for x. |
|
Students should be reminded
that when they complete the square, they should make sure that they are careful
with the sign on the x-term when they multiply by one-half. If they lose
that sign, they can get the wrong answer in the end, because they might forget
what goes inside the parentheses. Also, careful not to be sloppy and wait to do
the plus/minus sign until the very end.
Example 2: Solve x2 + 6x 7 = 0 by
completing the square.
Do the same procedure as
above, in exactly the same order. (Study tip: Always working these problems in
exactly the same way will help you remember the steps when you're taking your
tests.)Elizabeth -2009 All Rights Reserved
|
This is the original equation. |
x2 + 6x 7 = 0 |
|
Move the loose number over to the other side. |
x2 + 6x = 7 |
|
Take half of the x-term (that is, divide it by two) (and
don't forget the sign!), and square it. Add this square to both sides of the
equation. |
|
|
Convert the left-hand side to squared form. Simplify the
right-hand side. |
(x + 3)2 = 16 |
|
Square-root both sides. Remember to do "±" on the
right-hand side. |
x + 3 = ± 4 |
|
Solve for "x =". Remember that the
"±" gives you two solutions. Simplify as necessary. |
x =
3 ± 4 |
Remind students if they are
not consistent with remembering to put the plus/minus in as soon as they take
square root both sides, then this is an example of the type of exercise where they
will get themselves in trouble. They will write your answer as "x =
3 + 4 = 1", and have no idea how they got "x = 7",
because they won't have a square root symbol "reminding" them that they
"meant" to put the plus/minus in. That is, if they miss, these easier
problems will embarrass themselves!
Example 3: Solvex2 + 6x10 = 0.
Apply
the same procedure as on the previous page:
|
This is the original equation. |
x2 + 6x10 = 0 |
|
Move the loose number over to the other side. |
x2 + 6x = 10 |
|
Take half of the coefficient on the x-term (that is, divide it
by two, and keeping the sign), and square it. Add this squares value to both
sides of the equation. |
x2 + 6x + 9= 10 +9 |
|
Convert the left-hand side to squared form. Simplify the
right-hand side. |
(x + 3)2 = 19 x + 3 = ± |
|
Square root both sides. Remember to put the "±" on the
right-hand side. |
x = ± |
|
Solve for "x =", and simplify as necessary. |
x = 3 ± |
Quadratic
Formula
After students successful
understanding of the process of completing the square, the next discussion would be on performing completing the square
for the generic quadratic equation written as ax2 + bx + c = 0. Here, the teacher can ask
students try to do it by themselves in their groups. With the assistance of the
teacher they might be able to come up with the quadratic formula.
Though it is understood that
there is a difficulty teacher might face (showing students how the Formula was
invented, and thereby giving an example of the usefulness of symbolic
manipulation), the computations involved are often a bit beyond the average
student at this point. But, if explained well any student could get it easily. Here
is what the teacher is looking for:
|
Deriving the Quadratic Formula starts by solving the general
quadratic equation ax2 + bx + c = 0,
a≠0. This is the original equation. |
ax2 + bx + c = 0 |
|
Move the loose number to the other side. |
ax2 + bx = c |
|
Divide through by whatever is multiplied on the squared term. Add the squared term to both sides. |
|
|
Simplify on the right-hand side; in this case, simplify by
converting to a common denominator. |
|
|
Convert the left-hand side to square form (and do a bit more
simplifying on the right). |
|
|
Square root both sides, remembering to put the "±" on
the right. |
|
|
Solve for "x =", and simplify as necessary. |
|
Conclusion
Whether students are working
symbolically (as in the last example) or numerically (which is the norm), the
key to solving by completing the square is to practice, practice and practice.
By so doing, the process will become a bit more "automatic", and they
will remember the steps when they are asked any time. Thus, teacher should give
practice exercises.
Practice
Exercises
1. Factorize the
following expressions:
a) 57x2
21 + 19 7x2
b) x4
16
c) 16 40x2
+ 9 + 4x2
d) 3x4
4x3h) (x 1)2
4
e) 5(x 8)2
+ 8 133
f) 24x2
36x + 30
g) 1 9(x + 3)2
2.
Solve
for the unknown in each of the following:
a) 5x (3x - 7) = 0
b)
12x2 3 = 0
c) 4x2
+ 6 = 11x
d)
(2x - 3)2 4 = 0
3.
Solve
for x in each of the following
a)3x2
11 = 14 13x2
b)
(x
1)2 4 = 0
c)3x2
14x = x2 13x
d)
3x2
= 10 13x
e)(x + 8)2
= 25
f) x2 + 2x = 8x
g)
5x2
+ 3 = 21 + 3x2
h)
2x2
+ x 14 2x2
4.
Use
completing the square to solve the following quadratic equations:
a) 2x2
5x + 3 = 0
b) 9x2 +
x + 1 = 0
c) 4x2 +
4x + 1 = 0
d) x2
5x 3 = 0
5. Which one of the following is an equivalent
form of the quadratic expression![]() ?
?