
Figure 1.1: Vector notation
|
Back Introduction
|
Home Cover Page
|
Top Unit One
|
Next Unit Two
|
Unit One: Vectors
By the end of this lesson students will be able to:
Starter activity:
Begin the lesson recapping the core points about physical quantities. Remind students they studied in grades 7 & 8 that physics is an experimental science and experiments requires measurements, and we usually use numbers attached to units to describe the results of measurements. Any number that is attached to an appropriate units used to describe a physical phenomenon quantitatively is called a physical quantity. For example, among physical quantities that describe you are your weight and your height.
Any number or set of numbers with appropriate units attached, used for a quantitative description of a physical phenomenon is called a physical quantity.
The simplest kind of physical quantity is one that can be completely specified by its magnitude, a single number, together with the units in which it is measured. Such a quantity is called a scalar and examples include temperature, time and density.
But many other important quantities in physics have a direction associated with them and cannot be described by a single number and a unit.
We may think of it as an arrow in space. A simple example is the motion of an airplane. To describe this motion completely, we must say not only how fast the plane is moving, but also in what direction. . A familiar example is force, which has a magnitude (strength) measured in Newton and a direction of application. Giving a complete description of a force means describing both how hard the force pushes or pulls on the body and the direction of the push or pull.
When a physical quantity is described by a single number, we call it a scalar quantity. In contrast, a vector quantity has both a magnitude (the "how much" or "how big" part) and a direction in space.
Main Activity:
To have a clear understanding more about vectors and how they combine, let us start with the simplest vector quantity, displacement. This involves two pieces of information –the distance between two points and also the direction of one point from the other. Displacement is simply a change in position of a point. (The point may represent a particle or any body.) In Fig below we represent the change of position from point PI to point P 2 by a line from PI to P 2, with an arrowhead at P 2 to represent the direction of motion. Displacement is a vector quantity because we must state not only how far the particle moves, but also in what direction.

Analytically, we usually represent a vector quantity such as displacement by a bold type letter, such as A in Fig. 1.1 or by putting an arrow above them, the latter being much used in handwritten work. Keep students remind them that vector quantities have different properties from scalar quantities; the arrow is a reminder that vectors have direction. In handwriting, vector symbols are usually written with an arrow above them (see Fig. 1.1). When you write a symbol for a vector, always write it with an arrow on top.
A vector may be geometrically represented by an arrow with length proportional to the magnitude. The direction of the arrow indicates the direction of the vector, the positive sense of direction being indicated by the point.
If two vectors have the same direction, they are parallel (collinear). If they have the same magnitude and the same direction, they are equal, no matter where they are located in space.
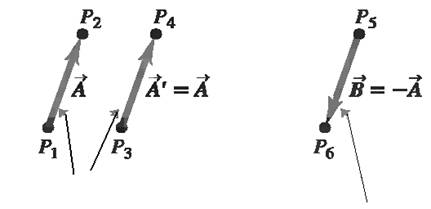
A and A’ are equal because they have the same length and direction. But displacement B has the same magnitude as A but opposite direction, that is the negative of A.
If two vectors have the same direction, they are parallel. If they have the same magnitude and the same direction, they are equal, no matter where they are located in space. The vector A' from point P3 to point P4 in Fig. 1.2 has the same length and direction as the vector A from P1 to P2 . These two displacements are equal, even though they start at different points. We write this as A' = A.
Two vector quantities are equal only when they have the same magnitude and the same direction.
The vector B in Fig. 1.2, however, is not equal to A because its direction is opposite to that of A. We define the negative of a vector as a vector having the same magnitude as the original vector but the opposite direction. The negative of vector quantity A is denoted as -A, and we use a boldface minus sign to emphasize the vector nature of the quantities. When two vectors A and B have opposite directions, whether their magnitudes are the same or not, we say that they are anti-parallel.
We usually represent the magnitude of a vector quantity by the same letter used for the vector, but in light italic type with no arrow on top, rather than boldface italic with an arrow (which is reserved for vectors). An alternative notation is the vector symbol with vertical bars on both sides:
(Magnitude of A) =A = |A|.
Throughout this material we will represent a vector in diagrams as a line together with an arrowhead. We will make no distinction between an arrowhead at the end of the line and one along the line’s length.
Concluding Activity:
A scalar is a quantity that is specified completely by a single number and a physical unit of measure. Scalars are quantities specified with units and are combined with the usual rules of arithmetic.
When the direction as well as the magnitude of a quantity must be quoted we are dealing with a vector quantity.
To represent a vector quantity diagrammatically, a line is drawn with length proportional to the magnitude of the vector quantity and with an arrow pointing in the same direction as the vector quantity. This allows geometry to be used to calculate the magnitude of unknown vector quantities, since the lengths of all lines in a vector diagram are proportional to the magnitudes of the vectors.
Stress the importance of getting in the habit of using the arrow symbols for vectors. If students often omit the vector arrow from the vector symbol they are more likely to be in confusion and mistakes.
After recapitulating the key ideas or concepts provide students with some carefully designed questions such as:
Support students in realizing that each is represented by only one number-the battery by 12V,the bottle by 1.5 Liter, the time by 2:35s and the weight by 67Kg ,and things described by a number with a unit are called scalars
Confirm that they come up the right answer as to supply travelling instructions and because it frequently useful to discuss the magnitude of the force or velocity without concerning ourselves with its directions to questions No 1 and 2 respectively.
Starter Activity:
Start the lesson informing students that they use vectors frequently, even if they may not be familiar with the term.”Run 3km northeast” or “walk 4m north, 2m east” are both vector descriptions. The name vector means carrier. In Biology a mosquito is a malaria vector. In physics the vector measures where a thing is carried 3m forward, 4m to the right and 5m up.
Main Activity:
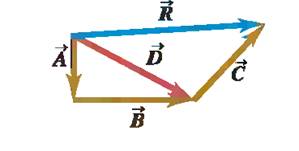
Vectors can be added or subtracted. In this lesson, we show how to do these operations graphically. It may be helpful to consider that these two vectors represent displacement. A women walks along displacement vector A and then along displacement vector B. Her initial point is the tail of A, and she would end up at the point at the end of A+B vector .The sum represent the displacement vector from her initial to final position .
To be more specific about the addition of process: we start with two vectors A and B, both drawn at the common origin. To add them, we move the vector B so it starts at the head of A. The sum is a vector that starts at the tail of A and ends at the head of B.
C = A + B (1.1)
Vector C is then represented by an arrow drawn from the tail of A to the tip point of B. This procedure, the triangle law of addition, assigns meaning to Eq. (1.1) and is illustrated in Fig. 1.3 bellow.
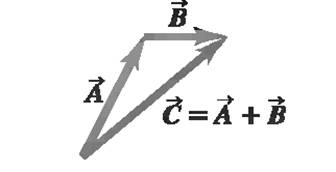
The sum A+ B of vectors A and B is defined as the vector directed from the initial point of A to the endpoint of B under the condition that B is applied at the endpoint of A. The rule for addition of vectors, which is contained in this definition, is called the triangle law of vector addition (see Fig. 1.3a.).
Subtraction is handled by defining the negative of a vector as a vector of the same magnitude but with reversed direction. Then
A − B = A + (−B) (1.2)
By completing the parallelogram (sketch it), we see that the sum A + B can also be found using the parallelogram law of vector addition- If vectors A and B are both drawn with their tails at the same point, vector C is the diagonal of a parallelogram constructed with A and B as two adjacent sides.
C = A + B = B + A. (1.3)
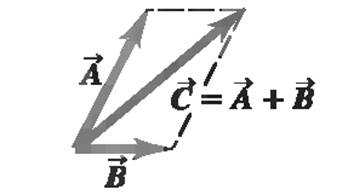
Common misconception-Magnitudes in vector addition
It's a common error to conclude that if C = A + B, then the magnitude C should just equal the magnitude A plus the magnitude B. In general, this conclusion is wrong; for the vectors shown in Fig. 1.3b, you can see that C < A + B. The magnitude of A + B depends on the magnitudes of A and B and on the angle between A and B). Only in the special case in which A and B are parallel is the magnitude of C = A + B equal to the sum of the magnitudes of A and B. By contrast, when the vectors are anti parallel the magnitude of C equals the difference of the magnitudes of A and B. If you are careful about distinguishing between scalar and vector quantities, you'll avoid making errors about the magnitude of a vector sum.
Give strong emphasis to the fact that the addition of vectors only makes physical sense if they are of a like kind, for example if they are both forces acting in three dimensions.
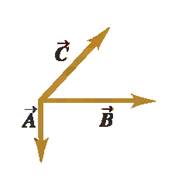
When we need to add more than two vectors, we may first find the vector sum of any two; add this vectori ally to the third, and so on. Figure 1.3c shows three vectors A, B, and C. In Fig 1.13c. We first add A and B to give a vector sum D; we then add vectors C and D by the same process to obtain the vector sum R:
R = (A + B) + C = D + C
To Verify the Parallelogram Law, let students in group perform the following experiment.
This experiment is carried out by applying three forces to a point and adjusting them until they are in equilibrium. When they are in equilibrium, their sum (as vectors) must be zero. The sum of any two of the vectors must then be equal and opposite to the third, to make the total sum of all three zero. We use the parallelogram law to find the resultant of two of the forces in the experiment, and show that this resultant is equal in magnitude and opposite in direction to the third force. This proves that the resultant found by the parallelogram law is the sum of the two vectors - especially when the experiment is repeated several times and a similar result is found each time.
As shown in the figure below (Figure: 1.4), the investigation explores the concept of equilibrium using forces on springs. Try to keep the spring scales as parallel as possible. Attach three springs to the loops of string with the key ring in the middle. Have three people each pull a spring, keeping the ring motionless with all the springs in a line.
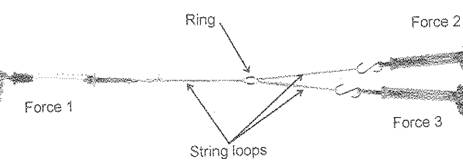
In the calculations, it is essential that the masses are converted to weights in Newton, What can you say about forces when nothing is moving? Notice that when nothing is moving it does not mean there are no forces acting. It means things are in equilibrium. In equilibrium the total (net) force is zero. What do your observations tell you about the relationship between the three forces acting on the ring? Let students draw a diagram showing the force vectors on the ring as arrows. Make the length of each arrow proportional to the strength of each force. For example,1 cm per 1N might be a reasonable length scale.
Concluding Activity:
Provide the class with a quiz and have quick check to see if they have understood the concepts introduced in the lesson. If students have trouble with the quiz, let them reread their textbook, ask their teacher for help, or discuss the material with a fellow student. A simple and yet useful and helpful quiz may look like:
Q1. List four quantities that are represented by vectors.
Q2. A ship sails northeast at a speed of 100m/s. Its velocity is V. What direction and speed would a boat with a velocity vector –V have?
Q3. A minibus travels from Addis Ababa to Gondar through Dessie town. A bus travels from Addis Ababa to Gondar by taking the route through Bahirdar .Do these two journeys have equal displacement vectors?
Q4. If the total force acting on an object is zero, does the object has to be at rest?
Objectives:
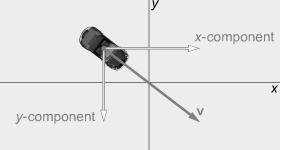
By defining a vector by its angle and magnitude, the magnitude and direction of the vector are stated separately. Three kilometers due north is an example. “Three kilometers” is the magnitude and “north” is the direction. The magnitude is always stated as a positive value. Instead of using “compass” or map directions, physicists use angles. Rather than saying “three kilometers north,” a physicist would likely say “three kilometers directed at 90 degrees.”
The angle is most conveniently measured by placing the vector’s starting point at the origin. The angle is then typically measured from the positive side of the x axis to the vector.
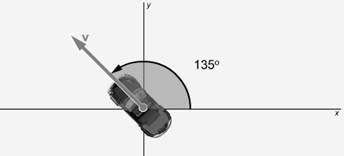
You see a car traveling northwest, with a vector indicating its velocity. Defining a vector by its angle and magnitude is one way to describe a vector. This notation states the two quantities (magnitude & direction) separately. Magnitude is the first part of this notation. In this case, it would be the speed of the car.
After magnitude, we need an angle to tell us which way to go. This gives us the direction of the vector, in this case the direction of the car’s velocity. In polar notation, the angle is measured from the positive x axis, as illustrated by the arc. An angle of 0° points directly to the right. Positive angles are in the counter-clockwise direction. Because the direction of the car is to the northwest (up and to the left), the value of the angle is between 90 and 180 degrees − to be precise, it is positive 135°.
For magnitude we use the letter v, since we are talking about velocity here. (For other quantities, other variables would be appropriate.) For angle, we use the Greek letter θ (theta). This is a common symbol for angles; you will see it often.
The way to write a vector in polar notation is (v, θ), in parentheses. First the magnitude (or length) of the vector is written, and then its direction
Let students attempt this question to express a velocity vector in polar notation.
Starter Activity:
In the preceding lessons we combined vectors graphically, but it is not an especially good way to find quantitative results. In this section we will introduce a coordinate description of vectors that will be the basis of an easier method of for doing vector calculations
We added vectors by using a scale diagram and by using properties of right triangles. Measuring a diagram offers only very limited accuracy, and calculations with right triangles work only when the two vectors are perpendicular. So we need a simple but general method for adding vectors. This is called the method of components.
To make the component method easy to understand, let us apply the analogy with a dance class, engaged with a preparation to win the Ethiopian Idol contest.. Ask the class if they have ever attended the dance class so that they may also help you.
If you were a dancer or a cheer leader you would easily understand the following choreography: “Take two steps forward, four steps to the right and one step back”. Note that these are vector instructions. If asked how far forward are after this dance move, you would say “one step”, which is two steps forward plus one step back Assist students to realize that their progress forward or back is unaffected by steps to the right or left. You correctly process left or right and forward or back separately.
Main Activity:
Frequently what we know, or want to know, about a particular vector is not its overall magnitude and direction, but how far it extends horizontally and vertically. On a graph, we represent the horizontal direction as x and the vertical direction as y. These are called Cartesian coordinates. The x component of a vector indicates its extent in the horizontal dimension and the y component its extent in the vertical dimension.
To define what we mean by the components of a vector A, we begin with a rectangular (Cartesian) coordinate system of axes (Fig1.5.). We then draw the vector with its tail at 0, the origin of the coordinate system. We can represent any vector lying in the xy-plane as the sum of a vector parallel to the x-axis and a vector parallel to the y-axis. These two vectors are labelled Ax and Ay" in Fig.; they are called the component vectors of vector A, and their vector sum is equal to A. In symbols,
A =Ax +Ay
Since each component vector lies along a coordinate-axis direction, we need only a single number to describe each one. When the component vector Ax points in the positive x-direction, we define the number Ax to be equal to the magnitude of Ax When the component vector AX points in the negative x-direction, we define the number AX to be equal to the negative of that magnitude (the magnitude of a vector quantity is itself never negative). We define the number AY in the same way. The two numbers AX and AY are called the components of A. (Fig.1.5)
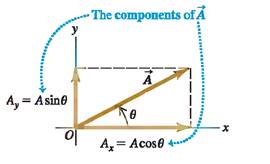
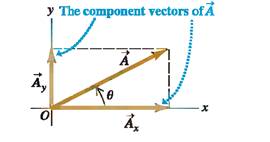
Figure: 1.5 Components of a vector
Common misconceptions: Components are not vectors
The components Ax and Ay of a vector A are not vectors themselves. This is why we print the symbols for components in light italic type with no arrow on top instead of the boldface italic with an arrow, which is reserved for vectors.
Let students beware of the confusing terminology Ax and Ay component vectors, where as Ax and Ay simply components. Make sure that you do not put arrow symbols over the components.
Concluding activity:
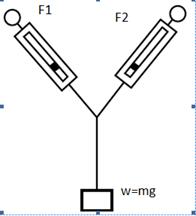
It is often convenient to replace a single vector by two component vectors .For example we may imagine a cupboard on a road being pulled by a woman using a rope inclined at an angle to the road and exerting a force F as shown below in the figure
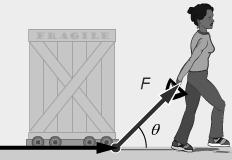
We may resolve the force F into two components at right angles to each other, FX along the Road and FY perpendicular to the road. We see at once if the law of vector addition is applied,
F = FX + FY
ACTIVITY:
Let the teacher provide students with following simple questions and confirm their understanding
Q1. Write the vectors labeled A, B and C with rectangular coordinates.
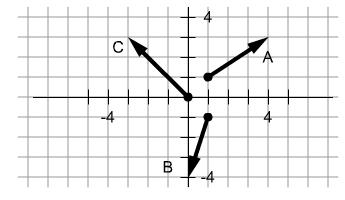
Q2. Write the vectors labeled V with rectangular coordinates
Give students a reading assignment on the application of vectors so that before coming to class, students are required to read related articles on reference materials as well as corresponding sections in the textbook.
Starter Activity: Having previously assigned the reading of the chapter as homework, initiate the class work by a discussion of the problem. Follow this with a consideration of force vectors acting at 00 and 1800 .Emphasize the definitions of components, resultant and equilibrant; then continue by the discussion and demonstrations listed below.
Main Activity Demonstration to verify the parallelogram law
This experiment is carried out by applying three forces to a point and adjusting them until they are in equilibrium. When they are in equilibrium, their sum (as vectors) must be zero. The sum of any two of the vectors must then be equal and opposite to the third, to make the total sum of all three zero.
We use the parallelogram law to find the resultant of two of the forces in the experiment, and show that this resultant is equal in magnitude and opposite in direction to the third force. This proves that the resultant found by the parallelogram law is the sum of the two vectors - especially when the experiment is repeated several times and a similar result is found each time.
Worked Example:
Find the x-and y-components of vector A =6 units shown in the figure below. Assume that vector a makes 300 with the X-axis
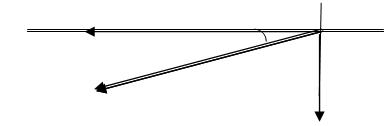
First decompose vector A into components parallel to the axes. The vector A=6 units ,300 below the negative x-axis, points to the left (negative x-direction)and down(negative y-direction).So the components Ax and Ay are both negative.
Ax = -Acos 300 = -(6 units) cos 300 = -5.2 units
Ay = -Asin300 = -(6 units) sin 300 = -3 units
Vectors are also useful and helpful in describing navigation. For example, an aircraft pilot makes use of the displacement vector when he states his position, and velocity vectors and laws of vector addition when deciding upon the direction to head the aircraft in order to arrive at a given destination
Note to the teacher on vectors: Vectors as things to be added by geometrical and analytical means seem clear, useful and helpful things to matured and motivated students. The students who first meet vectors at an early stage in physics may find them odd and difficult; and almost impossible to understand. Since the sense of difficulty disappears completely as time goes on, we urge teachers not to press any discussion on vectors beyond what seems sensible to their students at each age.