Unit 2: Topic 2: Equations Involving Radicals

Competencies

· Solve equations involving radicals

· Write solutions of equations involving radicals

Suggested ways of teaching this topic: Teacher guided group discussion

Starter Activities

The teacher may start raising brainstorming questions of the following type:

· “For what value(s) of x will x² = 16? ;2^x = 16?”

· What is the difference between x² = 16 and 2^x = 16

· What is the difference between x² = 16 and x = ?

· What do you think is the solution of = 16?

And, let the students come up with answers discussing in pairs or in small groups.

Expected Answers:

· x² = 16 for x = 4 and x = -4 ; 2^x = 16 for x = 4 only

· They have different solutions

· x² = 16 for x = 4 and x = -4 ; x = for x = 4 only. So, they have different solutions

· = 16 is true if x = 16² = 256.

The teacher then shall explain equations of the last form are radical equations and in this lesson students will solve equations that have the variable under a radical sign. At this stage, it is also better to inform students that they will be introduced to the concept of extraneous roots and see the necessity of checking all solutions by substituting them back into the original equation.

Lesson Notes

An equation that has a variable in a radicand is called a radical equation. The following are some examples of radical equations:

; ; ;

To solve an equation having a term with a variable in a radicand, start by "isolating" such a term on one side of the equation. Then raise the expression on each side of the equal sign to a power equal to the index of the radical. This is shown in the examples below.

Example 1: Solve the following equation

Solution:

= 7 – 3

= 4

x = 16 (squaring both sides)

(Substitute x = 16 in the original equation and see if it gives a true statement)

+ 3 = 7

which is true!

Example 2: Solve:

Solution:

4 = 7 + 9

4 = 16

= 4

5x -1 = 16 (squaring both sides)

5x = 17

(Substitute x = 17/5 in the original equation and see if it gives a true statement)

4 - 9 = 7

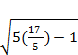4 – 9 = 7

16 – 9 = 7; which is true!

The teacher may pose a question: “In Examples 1 and 2 above we checked our solution. We did not stress the necessity of checking our solutions. Why are we doing this now?”

Answer:

Actually, checking solutions is a good practice to follow regardless of the type of equation you are solving. We should have done it when solving these other equations too. However, it is especially important to check solutions when solving radical equations because of the process of squaring both sides. The process of squaring can introduce unacceptable or extraneous roots. Because squaring can introduce these extraneous roots, it is essential we check the solutions we find to any equation that involves squaring both sides. Let’s see the following example:

Example 3: Solve:

Solution:

= x + 3

4x + 17 = x²+ 6x + 9

x²+ 2x - 8 = 0

x = -4 or x = 2

(Substitute x = -4 and x =2 in the original equation and see which of these give atrue statement)

- 3= -4

1- 3 = - 4 (This is wrong!)

can’t be a solution. (We call x = - 4 extraneous solution)

- 3= 2

5 – 3 = 2 ((This is correct!)

Is a solution.

Multiple Radicals - (Optional! The teacher could use this for brighter students)

Sometimes, a radical equation contains more than one term with a variable in a radicand. When this happens, you have to "isolate and raise to a power" more than once. Generally speaking it is better to isolate the more complicated radical first, as this can simplify the process of raising the expressions to a power.

Example 1: Solve: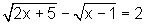

Solution:

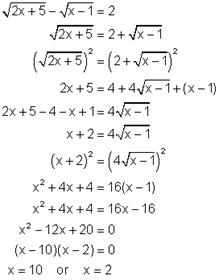
Check! (Substitute both x = 10 and x = 2 and see if you get true statements)

For x = 10,

For x = 2,

So, the solution is x = 10 and x = 3

Example 2: Solve:

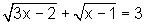
Solution:

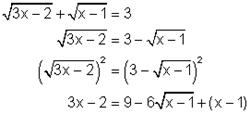
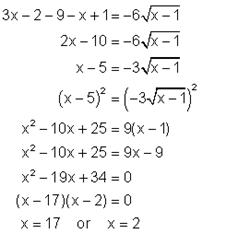
Check!

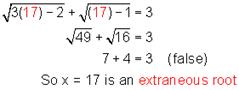
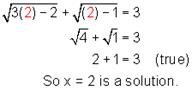
Concluding Activities

Make sure that the students got the idea of solving radical equations asking them to tell you the general format of solving these types of equations. The students are expected to tell you the following summary:

Equation involving radicals can be solved by squaring both sides, to eliminate the radical, and then solve for the value of the variable. Always checking the value obtained on the original equation is important to avoid extraneous roots in writing the solution.

Practice Exercise

1. Solve each of the following equations:

2. Solve each of the following equations:

10.

11.

12.

13.

14.

15.

16.