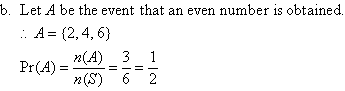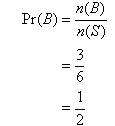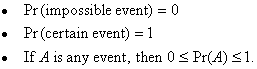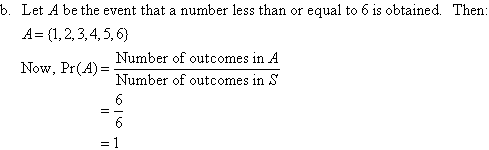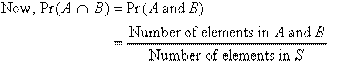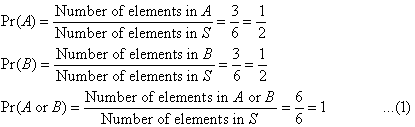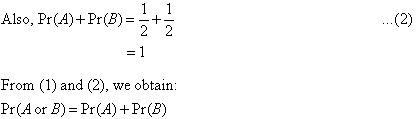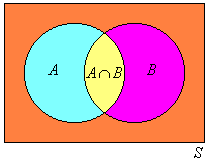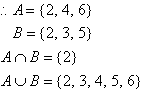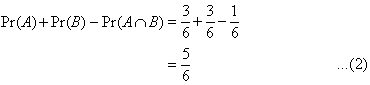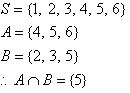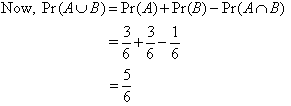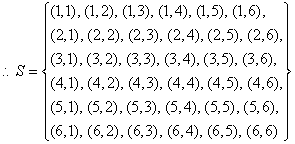Back Home Top

Unit 6: Topic 3: Probability of Events

Competencies

·   Determine the set of all possible outcomes

·   Find the probability of different events

·   Apply tree diagrams to determine outcomes of experiments

Suggested Methods of Teaching The Topic: Teacher explanation, small group activities

Starter Activities

The teacher could start with recalling Q & A session, asking the following:

·      What do we mean by sample space or possibility set?

·      What is an event? Give examples for each

Expected Answers

The sample space (S) of an experiment is the set of all possible outcomes of any trial of the experiment to be conducted.

An event (E) is a subset of the sample space. That is, an event is a subset of all possible outcomes. We refer to this subset of outcomes as favorable outcomes.

For example, the sample space for an experiment of tossing a fair coin is S = {H, T}, and the two possible outcomes are the events E1 = {H} and E2 = {T}.

Note that E1 is the event that 'a head falls' and E2 is the event that 'a tail falls'.

Lesson Notes

Probability of an Event

The probability of event E occurring is given by

Pr(E) = Number of outcomes in event E / Number of outcomes in sample space S

This is often written as:

Pr(E) = n(E) / n(S)

This result holds only if the outcomes of an experiment are equally likely.

Note: The events are denoted by capital letters A, B, C, D, E, ...

 

Example 1:  A die is rolled. Find:

a) the sample space for this experiment
b) the probability of obtaining an even number
c) the probability of obtaining a prime number

Solution:

A die.

 

(a) S = {1, 2, 3, 4, 5, 6}

(b) Let A be the event that an even number is obtained. Therefore, A = {2, 4, 6}. Pr(A) = n(A) / n(S) = 3 / 6 = 1 / 2

(c) Let B be the event that a prime number is obtained. Therefore, B = {2, 3, 5}

Pr(B) = n(B) / n(S) = 3 / 6 = 1 / 2

Range of Probability

If an event is impossible, its probability is 0. If an event is certain to occur, its probability is 1. The probability of any other event is between these two values. That is:

Pr(impossible event) = 0, Pr(certain event) = 1 and if A is any event, then 0 <= Pr(A) <= 1.

The probabilities for an impossible event, even chance and a certain event are 0, 1 / 2 and 1 respectively.

 

Example 2: A die is rolled. Find the probability of obtaining:

a)      A 7

b)      A number less than or equal to 6

Solution:

S = {1, 2, 3, 4, 5, 6}

(a) It is impossible to obtain a 7. So, Pr(7) = 0

(b) Let A be the event that a number less than or equal to 6 is obtained. Then A = {1,2,3,4,5,6}. Now, Pr(A) = Number of outcomes in A / Number of outcomes in S = 6 / 6 = 1

Note:

·         It is certain that event A will occur as it contains all 6 possible outcomes.

·         7 is not an outcome of rolling a die as it is not possible.

Example 3:

A pack of 52 playing cards consists of four suits, i.e. clubs, spades, diamonds and hearts. Each suit has 13 cards which are the 2, 3, 4, 5, 6, 7, 8, 9, 10, jack, queen, king and the ace card. Clubs and spades are of black color whereas diamonds and hearts are of red color. So, there are 26 red cards and 26 black cards. Find the probability of drawing from a well-shuffled pack of cards:

A)    A black card

B)    The king of diamonds

C)    A jack

Solution:

(a) A pack of 52 cards has 26 black cards. So, Pr(a black card) = 26/52 = 1/2

(b) A pack of 52 cards has 1 king of diamonds. So, Pr(the king of diamonds) = 1 / 52

(c) A pack of 52 cards has 4 jacks. So, Pr(a jack) = 4/52 = 1 / 13

Complement of Event A

A' is the complement of event A. It contains all of the elements in the sample spaceS that are not included in A.

A Venn diagram depicting the event A and its complement A'.

It is certain that either A or A' must occur. So, it follows that:

For any event A and its complement A':

Pr(A) + Pr(A') = 1

Example 4:

The probability that a train will be late is .  Find the probability that it will be on time.

Solution: Let A be the event that a train will be late. Then A' is the event that it will be on time.

Pr(A) + Pr(A') = 1 so Pr(A') = 99/100Pr(A) + Pr(A') = 1 so Pr(A') = 99/100Pr(A) + Pr(A') = 1 so Pr(A') = 99/100

 

 

 

 

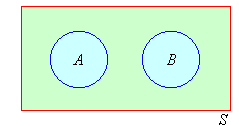
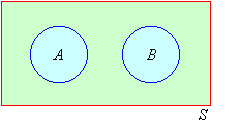
A and B are said to be mutually exclusive events if they do not overlap. This means that A and B are mutually exclusive events such that if A occurs then B is excluded or if B occurs then A is excluded. That is, A and B cannot occur together.

The Venn diagram shows events A and B are mutually exclusive events.

Note: Mutually exclusive events have no sample points in common.

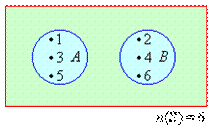
Consider the experiment of throwing a die. Let A be the event that an odd number is obtained and B be the event that an even number is obtained. Then:

A = {1, 3, 5}, B = {2, 4, 6}, Therefore A intersection B = the null set

That is, A and B have no elements (sample points) in common. Hence A and B are mutually exclusive events, as shown in the following Venn diagram.

The Venn diagram shows events A and B are mutually exclusive events. Event A contains the elements 1, 3 and 5 and event B contains the elements 2, 4 and 6. The number of elements in the sample space is 6.  Now, Pr(A intersection B) = Pr(A and B) = Number of elements in A and B / Number of elements in S = 0 / 6 = 0

Now, Pr(A intersection B) = Pr(A and B) = Number of elements in A and B / Number of elements in S = 0 / 6 = 0  = 0

Addition Law of Probabilities:  For the example under consideration: Pr(A) = Number of elements in A / Number of elements in S = 3/6 = 1/2, Pr(B) = Number of elements in B / Number of elements in S = 3/6 = 1/2, Pr(A or B) = Number of elements in A or B / Number of elements in S = 6/6 = 1 ...(1)

 

Also, Pr(A) + Pr(B) = 1/2 + 1/2 = 1 ...(2) From (1) and (2), we obtain: Pr(A or B) = Pr(A) + Pr(B)


Note:Pr(A or B) is also denoted by Pr(A U B).
In general:

1. If A and B are mutually exclusive events, then Pr(A U B) = Pr(A) + Pr(B)

The Venn diagram shows events A and B are mutually exclusive events.

If A and B overlap then,

2. If A and B overlap, then Pr(A U B) = Pr(A) + Pr(B) - Pr(A intersection B)

The Venn diagram shows the respective sample space for events A and B have some common elements.

Consider the experiment of throwing a die. As usual:

 

S = {1, 2, 3, 4, 5, 6}

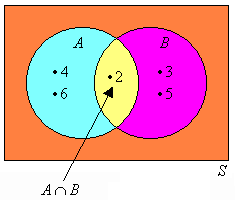
Let the events be defined as follows:

A = the event that an even number is obtained; and
B = the event that a prime number is obtained.

So A = {2, 4, 6}, B = {2, 3, 5}, A intersection B = {2}, A U B = {2, 3, 4, 5, 6}

The Venn diagram shows events A and B have the sample space element 2 in common. The sample space elements 4 and 6 are exclusive to event A and the sample space elements 3 and 5 are exclusive to event B.

 


Pr(A U B) = Number of elements in A U B / Number of elements in S = 5/6 ...(1), Pr(A) = 3/6, Pr(B) = 3/6, Pr(A intersection B) = 1/6

We notice that:

Pr(A) + Pr(B) - Pr(A intersection B) = 3/6 + 3/6 - 1/6 = 5/6

From (1) and (2), we obtain:

Pr(A U B) = Pr(A) + Pr(B) - Pr(A intersection B)

This is called the addition law of probabilities.

Example 5:

A die is rolled. If A = {greater than 3} and B = {prime}, find Pr(A or B).

Solution:

S = {1, 2, 3, 4, 5, 6}, A = {4, 5, 6}, B = {2, 3, 5}. So, A intersection B = {5}.

Now, Pr(A U B) = Pr(A) + Pr(B) - Pr(A intersection B) = 3/6 + 3/6 - 1/6 = 5/6

 

 

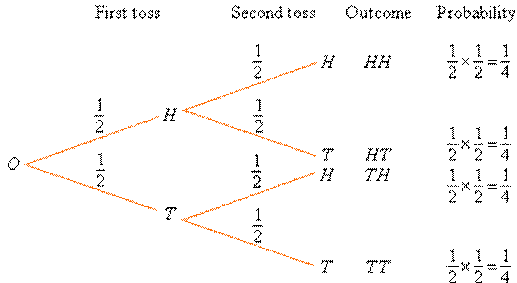
A tree diagram showing the possible outcomes and probabilities from tossing two coins.

 

So, far, we have mainly considered simple probability experiments such as tossing a coin or throwing a die. Usually, probability experiments are more complicated. For example, tossing two different coins, tossing a coin and throwing a die, or tossing the same coin three times etc.

Recall the experiment of tossing a coin twice where we are interested in the number of heads. The tree diagram is shown below.

Note that the tree diagram representation of this experiment involves two parts, 'the first toss of the coin' and 'the second toss of the coin'. Experiments that have two parts can be represented in tabular form.

For example, the following table uses rows to represent 'the first toss of the coin' and columns to represent 'the second toss of the coin'. The experiment's outcomes are shown in the bottom right-hand corner of the table where the rows and columns intersect.

The outcomes from the first toss of the coin are H and T and are shown vertically and the outcomes from the second toss of the coin are H and T and are shown horizontally. The resulting elements in the sample space for two coin tosses are HH, HT, TH, TT.

That is, S = {HH, HT, TH, TT}. Clearly, Pr(two heads) = 1/4, Pr(one head) = 2/4 = 1/2, Pr(no head) = 1/4

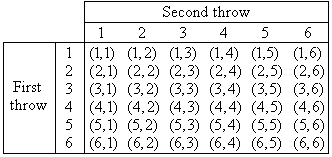
Example 6: Two dice are thrown. Let the events be defined as follows:

A = the numbers facing upwards on the two dice are the same
B = the sum of the numbers facing upwards on the two dice is 10
C = the sum of the numbers facing upwards on the two dice is 13

Find:

(a) Pr(A) (b) Pr(B) (c) Pr(A U B) (d) Pr(A intersection B) (e) Pr(C)

Solution:

Two dice are thrown. So, there are 36 elements in the sample space as shown in the table below.

The outcomes from the first die thrown are 1, 2, 3, 4, 5 and 6 and are shown vertically and the outcomes from the second die thrown are 1, 2, 3, 4, 5 and 6 and are shown horizontally. The resulting elements in the sample space for the two dice thrown are (1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5) and (6,6).

S = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}

n(S) = 36

(a) A = {(1,1), (2,2), (3,3), (4,4), (5,5), (6,6)}, Pr(A) = n(A)/n(S) = 6/36 = 1/6 (b) B = {(6,4), (5,5), (4,6)}, Pr(B) = n(B) / n(S) = 3/36 = 1/12 (c) A U B = {(1,1), (2,2), (3,3),(4,4), (5,5), (6,6), (6,4), (4,6)}, Pr(A U B) = n(A U B) / n(S) = 8/36 = 2/9 (d) A intersection B = {(5,5)}, Pr(A intersection B) = n(A intersection B) / n(S) = 1/36 (e) C = null set, Pr(C) = n(C) / n(S) = 0/36 = 0

 

Practice Exercises

1.      A lady has 3 dresses, 4 skirts and 5 blouses in her wardrobe. She decides to pack 2 dresses, 3 skirts and 3 blouses in her suitcase for her holiday. How many different choices can she make?

2.      A group of 12 people are waiting to board a taxi. The first taxi to arrive can only transport 4 of them. The following taxi can transport 5 of them and the third taxi can seat the remainder. In how many ways can the group be transported?

3.      A brother and sister and 5 other people are seated at random in a row at a concert. What is the probability that the brother and sister sit next to each other?

4.      A student buys sweets at the shop. On display are 3 chocolates, 4 toffees, 3 lollipops and 2 jellybeans, all of them different. In how many ways can the student choose 6 sweets of which 2 are chocolates and 1 is a toffee?

5.      How many four-digit numbers can be formed from the digits 2, 3, 4, 5, 6, and 7

a)      Without repetition?

b)      With repetition?

6.         How many ways are there to deal a five -card hand consisting of three eight's and two sevens from a full deck of 52cards?