Unit 1: The Real
Number System
Topic 1: Expressing Repeating Decimals as Fractions
Competencies
·
Express
repeating decimals as fraction
·
Show
that repeating decimals are also rational numbers
Suggested ways of teaching this
topic: Presentation and Explanation by
the Teacher
This is a formal teaching method which involves the teacher
presenting and explaining mathematics to the whole class. It can be difficult
because you have to ensure that all students understand. This can be a very
effective way of:
·
Teaching
a new piece of mathematics to a large group of students
·
Drawing
together everyone’s understanding at certain stages of a topic
·
Summarizing
what has been learnt
As a brain
storming activity you may ask students to
·
List
the types of decimals they know
·
Give
some examples of repeating decimals
Then, you might
start with a question like:
‘How can I
express ![]() as a fraction?’
as a fraction?’
Then, using
examples, you can show them how!
Lesson Notes
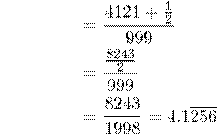
Let ![]()
Multiplying the
above equation by 1000(where there are 3 repeating decimals), we can have:
![]()
Subtracting x from 1000x, we get

Example 1:
Find
the fraction represented by the repeating decimal ![]() .
.
Let
n stand for ![]() or 0.77777 … So 10 n stands for
or 0.77777 … So 10 n stands for ![]() or 7.77777 …
or 7.77777 …
10
n and n have the same fractional part, so their difference is an
integer.
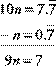
You
can solve this problem as follows.
![]()
So, ![]()
Example 2:
Find
the fraction represented by the repeating decimal ![]() .
.
Let
n stand for ![]() or 0.363636 … So 10 n stands for
or 0.363636 … So 10 n stands for ![]() or 3.63636 … and 100 n stands for
or 3.63636 … and 100 n stands for ![]() or 36.3636 …
or 36.3636 …
100
n and n have the same fractional part, so their difference is an
integer. (The repeating parts are the same, so they subtract out.)

You
can solve this equation as follows:
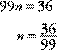 Now simplify
Now simplify ![]() to
to ![]() . So
. So ![]()
Example 3:
Find
the fraction represented by the repeating decimal ![]() .
.
Let
n stand for ![]() or 0.544444 … So 10 n stands for
or 0.544444 … So 10 n stands for ![]() or 5.444444 … and 100 n stands for
or 5.444444 … and 100 n stands for ![]() or 54.4444 …
or 54.4444 …
Since
100 n and 10 n have the same fractional part, their difference is
an integer. (Again, notice how the repeated parts must align to subtract out.)
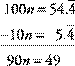
You
can solve this equation as follows.
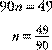
So, ![]()
Concluding Activities
Make
sure that students arrive at the following conclusive statements
Every decimal
numeral which is either
·
A terminating decimal number, or
·
A repeating non terminating decimal number, can be expressed as a fraction.
And
conversely, every fractional number represents a terminating, or repeating non
–terminating decimal number.
Practice Exercises
Find the
rational number represented by each of the following:
·
0.1![]()
·
0.7![]()
·
3.![]()
·
0.![]()